Neocijenjeno
8. rujna 2023. 20:21 (2 godine, 6 mjeseci)
Neka su
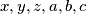
cijeli brojevi za koje vrijedi:
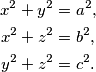
Dokažite da je broj
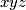
djeljiv s


,

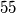
.
%V0
Neka su $x,y,z,a,b,c$ cijeli brojevi za koje vrijedi:$$$\begin{align*}
x^2+y^2&=a^2\text{,} \\
x^2+z^2&=b^2\text{,} \\
y^2+z^2&=c^2\text{.} \\
\end{align*}$$$ Dokažite da je broj $xyz$ djeljiv s
$(a)$ $5$,
$(b)$ $55$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
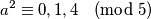 Očito ne mogu sva tri imat ostatak
Očito ne mogu sva tri imat ostatak 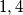 jer onda zbroj 2 s istim nebi bio kvadratni ostatak.
jer onda zbroj 2 s istim nebi bio kvadratni ostatak.
Analogno dokažeš da jedan mora biti djeljiv s  samo šta ima više ostataka. Tako da npr uzmeš prvi ostatak pa vidiš koje ostatke mogu imat ostala 2 (uvik ce bit samo 2 mogucnosti) i dokažeš da za te ostatke kad zbrojis iste ili razlicite nes nikad dobit kvadratni ostatak mod 11
samo šta ima više ostataka. Tako da npr uzmeš prvi ostatak pa vidiš koje ostatke mogu imat ostala 2 (uvik ce bit samo 2 mogucnosti) i dokažeš da za te ostatke kad zbrojis iste ili razlicite nes nikad dobit kvadratni ostatak mod 11
$$a^2 \equiv 0 , 1 , 4 \pmod 5$$
Očito ne mogu sva tri imat ostatak $1 , 4$ jer onda zbroj 2 s istim nebi bio kvadratni ostatak.
Analogno dokažeš da jedan mora biti djeljiv s $11$ samo šta ima više ostataka.
Tako da npr uzmeš prvi ostatak pa vidiš koje ostatke mogu imat ostala 2 (uvik ce bit samo 2 mogucnosti) i dokažeš da za te ostatke kad zbrojis iste ili razlicite nes nikad dobit kvadratni ostatak mod 11
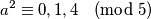 Očito ne mogu sva tri imat ostatak
Očito ne mogu sva tri imat ostatak 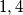 jer onda zbroj 2 s istim nebi bio kvadratni ostatak.
jer onda zbroj 2 s istim nebi bio kvadratni ostatak. samo šta ima više ostataka. Tako da npr uzmeš prvi ostatak pa vidiš koje ostatke mogu imat ostala 2 (uvik ce bit samo 2 mogucnosti) i dokažeš da za te ostatke kad zbrojis iste ili razlicite nes nikad dobit kvadratni ostatak mod 11
samo šta ima više ostataka. Tako da npr uzmeš prvi ostatak pa vidiš koje ostatke mogu imat ostala 2 (uvik ce bit samo 2 mogucnosti) i dokažeš da za te ostatke kad zbrojis iste ili razlicite nes nikad dobit kvadratni ostatak mod 11  Školjka
Školjka 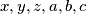 cijeli brojevi za koje vrijedi:
cijeli brojevi za koje vrijedi: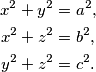 Dokažite da je broj
Dokažite da je broj 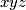 djeljiv s
djeljiv s
 ,
,
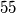 .
.