Neocijenjeno
9. rujna 2023. 15:40 (1 godina, 2 mjeseci)
Odredi sve prirodne brojeve
takve da je umnožak svih pozitivnih djelitelja broja
jednak
.
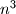
Prikaži ih u kanonskom obliku, tj. pomoću rastava na proste faktore.
%V0
Odredi sve prirodne brojeve $n$ takve da je umnožak svih pozitivnih djelitelja broja $n$ jednak $n^3$.
Prikaži ih u kanonskom obliku, tj. pomoću rastava na proste faktore.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Zato što znamo da broj ima djelitelje
$$1 , a_1 , a_2 , .... , \frac{n}{a^2} , \frac{n}{a^2} , n$$
Zaključujemo da $n$ ima 6 faktora. Tjst $n = p^2q$
Školjka 
Zaključujemo da 