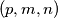
Odredi sve trojke prirodnih brojeva takve da je prost broj i da vrijedi
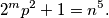
%V0
Odredi sve trojke prirodnih brojeva $(p, m, n)$ takve da je $p$ prost broj i da vrijedi $$
2^m p^2 + 1 = n^5 \text{.}
$$
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Faktorizacija Uočimo da taki da su ta dva broja relativno prosta. Desna strana je djeljiva s 8 pa mora bit i ljeva. je očito neparan broj a Odavde imamo I na kraju dobijemo rješenje
Faktorizacija
$$(n - 1)(n^4 + n^3 + n^2 + n + 1) = 2^mp^2$$
$M(n - 1 , n^4 + n^3 + n^2 + n + 1) | 5$
Uočimo da $n \neq 1$ taki da su ta dva broja relativno prosta.
$$n = 2^m + 1$$
$$n(n^3 + n^2 + n + 1) = (p - 1)(p + 1)$$
Desna strana je djeljiva s 8 pa mora bit i ljeva. $n$ je očito neparan broj a
$$n^3 + n^2 + n + 1 \equiv 4 \pmod 2^m$$
Odavde imamo $m < 3$
I na kraju dobijemo rješenje
$$(p , m , n) = (11 , 1 , 3)$$
Školjka 
takve da je 
prost broj i da vrijedi 
Uočimo da 
taki da su ta dva broja relativno prosta. 
Desna strana je djeljiva s 8 pa mora bit i ljeva. 
je očito neparan broj a 
Odavde imamo 
I na kraju dobijemo rješenje 