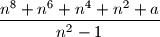
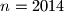
Odredi najmanji prirodni broj takav da je vrijednost izraza za cijeli broj djeljiv sa .
%V0
Odredi najmanji prirodni broj $a$ takav da je vrijednost izraza $$\frac{n^8+n^6+n^4+n^2+a}{n^2-1}$$ za $n = 2014$ cijeli broj djeljiv sa $3$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Očito je nazivnik djeljiv s i nije djeljiv s Tako da bi brojnik bio djeljiv s Da bi ovo uopce bio cjeli broj mora vrijedit. Očito to možemo vidjet ali zato Radi. i za najmanji moguć
Očito je nazivnik djeljiv s $3$ i nije djeljiv s $9$
$a = 9k + 2$
Tako da bi brojnik bio djeljiv s $9$
Da bi ovo uopce bio cjeli broj mora vrijedit.
$$n^2 - 1 | a + 4$$
Očito $a + 4 \neq n^2 - 1$ to možemo vidjet $mod 9$ ali zato $a + 4 = 2(n^2 - 1)$
$$a = 2n^2 - 6$$
Radi. $a \equiv 2 \pmod 9$ i $a = (n^2 - 1)k - 4$ za najmanji $k$ moguć
Školjka 
takav da je vrijednost izraza 
za 
cijeli broj djeljiv sa 
. 
Tako da bi brojnik bio djeljiv s 
Očito 
to možemo vidjet 
ali zato 
Radi. 
i 
za najmanji 
moguć