Točno
9. rujna 2023. 21:40 (8 mjeseci)
Odredi sve parove prirodnih brojeva $(a,b)$ za koje $a^2b$ dijeli $b^2 + 3a$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Amo stavit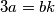 
, 
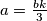
Onda dobijemo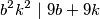 
Za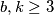 
ovo nema rješenja. Tako da trebamo samo probat za 
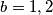rješenja su simetrična.
Na kraju dobijemo rješenja
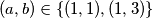
Amo stavit $3a = bk$ , $a = \frac{bk}{3}$
Onda dobijemo
$$b^2k^2 \ | \ 9b + 9k$$
Za $b , k \geq 3$ ovo nema rješenja.
Tako da trebamo samo probat za $b = 1 , 2$ rješenja su simetrična.
Na kraju dobijemo rješenja
$$(a , b) \in \{(1 , 1) , (1 , 3)\}$$
Školjka 
za koje 
dijeli 
.