Neocijenjeno
10. rujna 2023. 14:07 (1 godina, 5 mjeseci)
Nađite sva rješenja
jednadžbe:
(
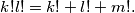
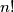
označava umnožak prirodnih brojeva od
do
.)
%V0
Nađite sva rješenja $k, l, m \in \mathbb{N}$ jednadžbe:
$$k!l! = k! + l! + m!\text{.}$$
($n!$ označava umnožak prirodnih brojeva od $1$ do $n$.)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Rješenje je $(k , l , m) = (3 , 3 , 4)$
Uvjerimo se da je $k = l$
Pretpodstavimo $k > l$
$$m! + 1 = (k! - 1)(l! + 1) \geq k! - 1$$
Imamo
$$m! \geq k! - 2$$
Za $k \geq 3$ očito vrijedi $m! \geq k!$
Onda iz početne jednađbe imamo $k! \ | \ l!$ odakle imamo $k = l$
Sad kad gledamo
$$k!(k! - 2) = m!$$
Za $k > 3$
$m! = (k + 2)!$ ili $m! = (k + 3)!$
To gledamo $v_2(m!) = v_2(k!) + 1$
A to očito nema rješenja. Dovoljno je pogledati prvih par. Na kraju $k! - 2$ raste puno više nego kvadrat ili kub.
Školjka 
Uvjerimo se da je 
Pretpodstavimo 
Imamo 
Za 
očito vrijedi 
odakle imamo 
Za 
ili 
To gledamo 
raste puno više nego kvadrat ili kub.