Neocijenjeno
10. rujna 2023. 16:56 (1 godina, 2 mjeseci)
Za dani prosti broj
odredi sve cijele brojeve
takve da je
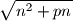
cijeli broj.
%V0
Za dani prosti broj $p$ odredi sve cijele brojeve $n$ takve da je $\displaystyle {\sqrt{n^{2}+pn}}$ cijeli broj.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Napišimo to kao
$$\sqrt{n(n + p)}$$
1° $M(n , p) = 1$
$n = k^2$
$$k^2 + p = m^2$$
$$k^2 = \frac{(p - 1)^2}{4}$$
Ovo je naravno samo za $p \neq 2$
2° $n = pk$
$$p\sqrt{k(k + 1)} \in \mathbb{Z}$$
$k = 0$
Edit : Očito previše radim s prirodnim brojevima pa mi je promaklo $n = -k^2$
Školjka 
1° 
Ovo je naravno samo za 
