Neocijenjeno
11. rujna 2023. 18:28 (2 godine, 6 mjeseci)
a) Dokažite da se ploča dimenzija
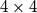
može obojiti u dvije boje tako da za svaki izbor dvaju redaka i dvaju stupaca vrijedi da četiri polja u presjecima tih redaka i stupaca nisu sva obojana istom bojom.
b) Dokažite da gore navedeno svojstvo ne vrijedi za ploču dimenzija
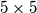
.
%V0
a) Dokažite da se ploča dimenzija $4 \times 4$ može obojiti u dvije boje tako da za svaki izbor dvaju redaka i dvaju stupaca vrijedi da četiri polja u presjecima tih redaka i stupaca nisu sva obojana istom bojom.
b) Dokažite da gore navedeno svojstvo ne vrijedi za ploču dimenzija $5 \times 5$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Za b) Svaki red ima barem 1 boju s 3 ili više polja. Takvih redaka koji imaju 3 ili više polja iste boje ih ima barem 3. Opet diriklerov princip. Tu ikamo kontradikciju već.
Za a) samo treba nacrtat jedan koji valja.
Naravno ovo rješenje nije dobro al nemogu baš puno s riječima reć
Za b)
Svaki red ima barem 1 boju s 3 ili više polja. Takvih redaka koji imaju 3 ili više polja iste boje ih ima barem 3. Opet diriklerov princip. Tu ikamo kontradikciju već.
Za a) samo treba nacrtat jedan koji valja.
Naravno ovo rješenje nije dobro al nemogu baš puno s riječima reć