Neocijenjeno
26. listopada 2023. 21:57 (2 godine, 4 mjeseci)
Brojevi
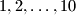
raspoređeni su u kružiće na slici, a zatim je u svaki od devet malih trokuta upisan zbroj brojeva upisanih u njegove vrhove.
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Dokaži da među brojevima upisanim u trokute postoje tri čiji je zbroj barem
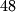
.
%V0
Brojevi $1,2,\ldots,10$ raspoređeni su u kružiće na slici, a zatim je u svaki od devet malih trokuta upisan zbroj brojeva upisanih u njegove vrhove.
[img attachment=3 width=150]
Dokaži da među brojevima upisanim u trokute postoje tri čiji je zbroj barem $48$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Naći ćemo očekivanu vrijednost zbroja brojeva u tri trokuta. Tojest oznaćimo brojeve upisane u trokutima sa $a$, $b$ , $c$. Sada tražimo :
\[\mathbb{E}(a + b + c) \]
Zbog linearnosti očekivane vrijednosti znamo da je :
\begin{align*}
\mathbb{E}(a + b + c) &= \mathbb{E}(a) + \mathbb{E}(b) + \mathbb{E}(c) \\
&= 3\mathbb{E}(a)
\end{align*}
Sada čemo pronaći oćekivanu vrijednost jednog trokuta. Zato što je mogućih kombinacija ${10 \choose 3}$ , a svaki broj se pojavljuje ${9 \choose 2}$ puta. Imamo :
\[\mathbb{E}(a) = \frac{{9 \choose 2} (1 + 2 + ... + 10)}{{10 \choose 3}} = 16.5\]
Iz ovoga zaključujemo da je za svaku kombinaciju ovih deset brojeva očekivana vrijednost :
\[\mathbb{E}(a + b + c) = 3 \cdot 16.5 = 49.5\]
Stoga zaključujemo da postoje $3$ trokuta čija je vrijednost veća od $48$.
 ,
,  ,
,  . Sada tražimo :
. Sada tražimo : 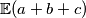
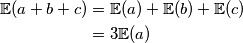
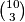 , a svaki broj se pojavljuje
, a svaki broj se pojavljuje 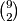 puta. Imamo :
puta. Imamo :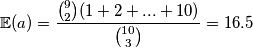
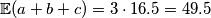
 trokuta čija je vrijednost veća od
trokuta čija je vrijednost veća od 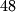 .
.  Školjka
Školjka 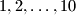 raspoređeni su u kružiće na slici, a zatim je u svaki od devet malih trokuta upisan zbroj brojeva upisanih u njegove vrhove.
raspoređeni su u kružiće na slici, a zatim je u svaki od devet malih trokuta upisan zbroj brojeva upisanih u njegove vrhove.