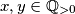Točno
5. rujna 2024. 14:00 (7 mjeseci)
Let $\mathbb{Q}_{>0}$ denote the set of all positive rational numbers. Determine all functions $f:\mathbb{Q}_{>0}\to \mathbb{Q}_{>0}$ satisfying $$f(x^2f(y)^2)=f(x)^2f(y)$$for all $x,y\in\mathbb{Q}_{>0}$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Označimo s 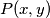 danu funkcijsku jednadžbu. Dokazat ćemo sljedeću tvrdnju:
danu funkcijsku jednadžbu. Dokazat ćemo sljedeću tvrdnju:
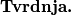
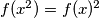 za sve
za sve 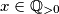
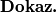
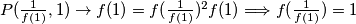
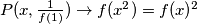
što dokazuje tvrdnju.
Posebno, imamo 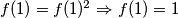
Nadalje, 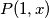 nam daje
nam daje 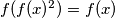 , a zbog tvrdnje vrijedi
, a zbog tvrdnje vrijedi 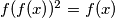 , što nam daje motivaciju da indukcijom dokažemo
, što nam daje motivaciju da indukcijom dokažemo
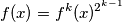
gdje 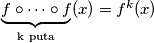 .
.
Baza je već riješena, 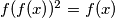
Pretpostavimo da za neki 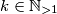 vrijedi
vrijedi

onda za  imamo
imamo
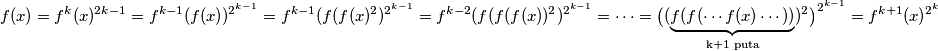
što dovršava korak indukcije.
Znači, imamo da je
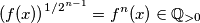
Iz čega slijedi da ako je  prost broj onda za svaki
prost broj onda za svaki  i sve prirodne brojeve
i sve prirodne brojeve 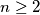 vrijedi
vrijedi
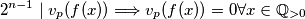
A to je jedino moguće ako  nema prostih faktora, tj.
nema prostih faktora, tj. 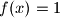 i to je to. Najssss!!!
i to je to. Najssss!!!
Označimo s $P(x,y)$ danu funkcijsku jednadžbu. Dokazat ćemo sljedeću tvrdnju:
$\textbf{Tvrdnja.}$ $f(x^2)=f(x)^2$ za sve $x\in\mathbb{Q}_{>0}$
$\textbf{Dokaz.}$
$P(\frac{1}{f(1)},1)\rightarrow f(1)=f(\frac{1}{f(1)})^2f(1)\Longrightarrow f(\frac{1}{f(1)})=1$
$P(x,\frac{1}{f(1)})\rightarrow f(x^2)=f(x)^2$
što dokazuje tvrdnju.
Posebno, imamo $f(1)=f(1)^2\Rightarrow f(1)=1$
Nadalje, $P(1,x)$ nam daje $f(f(x)^2)=f(x)$, a zbog tvrdnje vrijedi $f(f(x))^2=f(x)$, što nam daje motivaciju da indukcijom dokažemo
$$f(x)=f^k(x)^{2^{k-1}}$$
gdje $\underbrace{f \circ \cdots \circ f}_{\text{k puta}}(x)=f^k(x)$.
Baza je već riješena, $f(f(x))^2=f(x)$
Pretpostavimo da za neki $k\in\mathbb{N}_{>1}$ vrijedi
$f(x)=f^k(x)^{2{k-1}}$
onda za $k+1$ imamo
$$f(x)=f^k(x)^{2{k-1}}=f^{k-1}(f(x))^{2^{k-1}}=f^{k-1}(f(f(x)^2)^{2^{k-1}}=f^{k-2}(f(f(f(x))^2)^{2^{k-1}}=\cdots=\big( (\underbrace{f(f( \cdots f(x) \cdots))}_{\text{k+1 puta}})^2\big)^{2^{k-1}}=f^{k+1}(x)^{2^k}$$
što dovršava korak indukcije.
Znači, imamo da je
$$\left(f(x) \right)^{1/2^{n-1}}=f^{n}(x) \in \mathbb{Q}_{>0}$$
Iz čega slijedi da ako je $p$ prost broj onda za svaki $x$ i sve prirodne brojeve $n\ge2$ vrijedi
$$2^{n-1}\mid v_p(f(x)) \Longrightarrow v_p(f(x))=0 \forall x\in\mathbb{Q}_{>0}$$
A to je jedino moguće ako $f(x)$ nema prostih faktora, tj. $f(x)=1$ i to je to. Najssss!!!
| 11. rujna 2024. 20:09 | Patrlk | Točno |
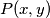 danu funkcijsku jednadžbu. Dokazat ćemo sljedeću tvrdnju:
danu funkcijsku jednadžbu. Dokazat ćemo sljedeću tvrdnju: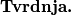
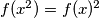 za sve
za sve 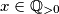
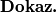
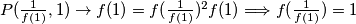
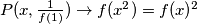
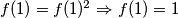
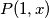 nam daje
nam daje 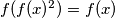 , a zbog tvrdnje vrijedi
, a zbog tvrdnje vrijedi 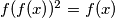 , što nam daje motivaciju da indukcijom dokažemo
, što nam daje motivaciju da indukcijom dokažemo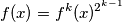
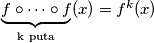 .
.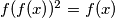
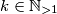 vrijedi
vrijedi
 imamo
imamo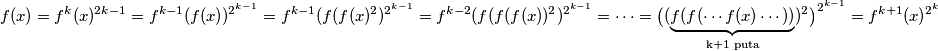
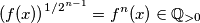
 prost broj onda za svaki
prost broj onda za svaki  i sve prirodne brojeve
i sve prirodne brojeve 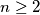 vrijedi
vrijedi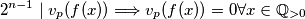
 nema prostih faktora, tj.
nema prostih faktora, tj. 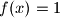 i to je to. Najssss!!!
i to je to. Najssss!!!  Školjka
Školjka 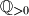 denote the set of all positive rational numbers. Determine all functions
denote the set of all positive rational numbers. Determine all functions 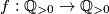 satisfying
satisfying 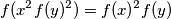 for all
for all