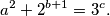Gledamo mod  .
.  daje
daje 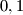 ,
, 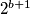 daje
daje 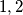 , jedina moguća kombinacija je
, jedina moguća kombinacija je 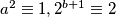 mod
mod  .
. 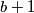 je neparan, odnosno
je neparan, odnosno  je paran.
je paran.
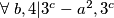 daje
daje 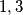 , a
, a  daje
daje 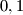 mod
mod  . Jedina moguća kombinacija je
. Jedina moguća kombinacija je 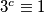 mod
mod  , odnosno
, odnosno 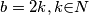
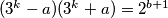
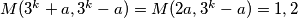 , zbog toga što je
, zbog toga što je  neparan.
neparan.
(1.)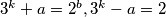
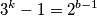 gledamo mod
gledamo mod  ,
, 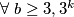 daje ostatak
daje ostatak  , pa je
, pa je 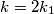
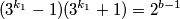
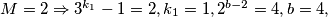
Dakle, za sve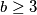 , jedino rješenje je
, jedino rješenje je 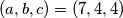
Sada samo moramo provjerit 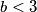
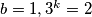 , nemoguce
, nemoguce
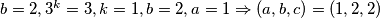
(2.)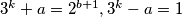
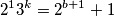
 ne dijeli
ne dijeli  , nemoguce.
, nemoguce.
(3.)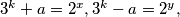
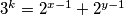 , neparni broj nije jednak parnom, pa
, neparni broj nije jednak parnom, pa  ili
ili  moraju biti
moraju biti  .
. ocito ne moze biti
ocito ne moze biti  , pa je onda
, pa je onda 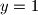 ,. Kako je
,. Kako je 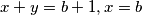 pa uvrstavanjem
pa uvrstavanjem 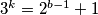 , no rješenje te jednadžbe smo vec našli.
, no rješenje te jednadžbe smo vec našli.
Jedina rješenja su 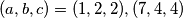
Gledamo mod $3$. $a^2$ daje $0,1$, $2^{b+1}$ daje $1,2$, jedina moguća kombinacija je $a^2\equiv 1, 2^{b+1}\equiv 2$ mod $3$. $b+1$ je neparan, odnosno $b$ je paran.
$\forall \; b,4|3^c-a^2, 3^c$ daje $1,3$, a $a^2$ daje $0,1$ mod $4$. Jedina moguća kombinacija je $3^c\equiv 1$ mod $4$, odnosno $b=2k, k\mathbb\in{N}$
$(3^k-a)(3^k+a)=2^{b+1}$
$M(3^k+a,3^k-a)=M(2a,3^k-a)=1,2$, zbog toga što je $a$ neparan.
(1.)$3^k+a=2^b, 3^k-a=2$
$$ 3^k-1=2^{b-1}$$
gledamo mod $4$, $ \forall\; b \ge 3, 3^k$ daje ostatak $1$, pa je $k=2k_1$
$$(3^{k_1}-1)(3^{k_1}+1)=2^{b-1}$$
$M=2\Rightarrow 3^{k_1}-1=2, k_1=1, 2^{b-2}=4, b=4,$
Dakle, za sve$ b\ge 3$, jedino rješenje je $(a,b,c)=(7,4,4)$
Sada samo moramo provjerit $b<3$
$b=1, 3^k=2$ , nemoguce
$b=2,3^k=3, k=1,b=2,a=1\Rightarrow (a,b,c)=(1,2,2)$
(2.)$3^k+a=2^{b+1}, 3^k-a=1$
$$2^13^k=2^{b+1}+1$$
$2$ ne dijeli $1$, nemoguce.
(3.)$ 3^k+a=2^x,3^k-a=2^y,$
$3^k=2^{x-1}+2^{y-1}$, neparni broj nije jednak parnom, pa $x$ ili $y$ moraju biti $1$.$x$ ocito ne moze biti $1$, pa je onda $y=1$,. Kako je $x+y=b+1, x=b$ pa uvrstavanjem $3^k=2^{b-1}+1$, no rješenje te jednadžbe smo vec našli.
Jedina rješenja su $(a,b,c)=(1,2,2),(7,4,4)$
 .
.  daje
daje 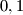 ,
, 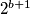 daje
daje 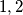 , jedina moguća kombinacija je
, jedina moguća kombinacija je 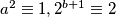 mod
mod  .
. 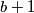 je neparan, odnosno
je neparan, odnosno  je paran.
je paran.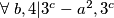 daje
daje 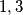 , a
, a  daje
daje 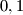 mod
mod  . Jedina moguća kombinacija je
. Jedina moguća kombinacija je 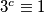 mod
mod  , odnosno
, odnosno 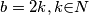
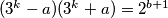
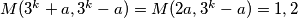 , zbog toga što je
, zbog toga što je  neparan.
neparan.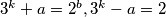
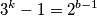 gledamo mod
gledamo mod  ,
, 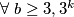 daje ostatak
daje ostatak  , pa je
, pa je 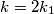
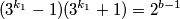
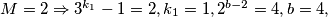
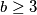 , jedino rješenje je
, jedino rješenje je 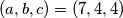
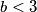
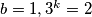 , nemoguce
, nemoguce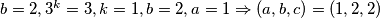
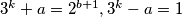
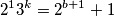
 ne dijeli
ne dijeli  , nemoguce.
, nemoguce.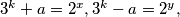
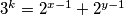 , neparni broj nije jednak parnom, pa
, neparni broj nije jednak parnom, pa  ili
ili  moraju biti
moraju biti  .
. ocito ne moze biti
ocito ne moze biti  , pa je onda
, pa je onda 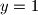 ,. Kako je
,. Kako je 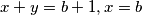 pa uvrstavanjem
pa uvrstavanjem 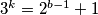 , no rješenje te jednadžbe smo vec našli.
, no rješenje te jednadžbe smo vec našli.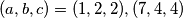
 Školjka
Školjka 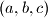 takve da vrijedi
takve da vrijedi