Neocijenjeno
22. rujna 2023. 18:07 (2 godine, 5 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Promjenimo malo zadatak : Nađimo sve 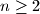 tako da za svaki
tako da za svaki 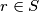 ,gdje je
,gdje je  reduced residue class od
reduced residue class od  ,
, 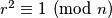 ovo je ekvivalentan zadatak onome.
ovo je ekvivalentan zadatak onome.
Sad dokažimo da 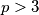 ne može djelit
ne može djelit  Koristit ćemo činjenicu da je reduced residue class od
Koristit ćemo činjenicu da je reduced residue class od  također reduced residue class od
također reduced residue class od  . Tako da postoji
. Tako da postoji 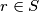 tako da je
tako da je 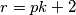
Sad iz pretpostavke 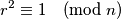 Imamo i
Imamo i 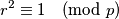 Za svaki
Za svaki  . Što je kontradikcija ako ubacimo
. Što je kontradikcija ako ubacimo 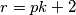 jer to bi znaćilo da je
jer to bi znaćilo da je 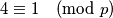 Za
Za 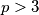 Odavde imamo da ne postoji nikakav prost broj veći od
Odavde imamo da ne postoji nikakav prost broj veći od  sad imamo da je
sad imamo da je 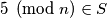 Tako da mora vrijediti :
Tako da mora vrijediti :
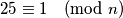 Ili ti
Ili ti 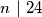 što i jesu sva rješenja kad provjerimo.
što i jesu sva rješenja kad provjerimo.
 Školjka
Školjka  and
and  relatively prime to
relatively prime to 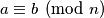 if and only if
if and only if 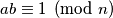 .
.