Neocijenjeno
22. rujna 2023. 21:39 (2 godine, 5 mjeseci)
Na ploču dimenzija
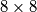
postavljaju se tromino-pločice oblika

tako da svaka tromino-pločica prekriva točni tri polja ploče, a međusobno se ne prekrivaju.
Koliko je najmanje tromino-pločica potrebno postaviti na ploču ako želimo da se nakon toga više ne može postaviti nijedna dodatna tromino-pločica.
%V0
Na ploču dimenzija $8 \times 8$ postavljaju se tromino-pločice oblika $
\setlength{\unitlength}{5pt}
\begin{picture}(2, 3)
\put(0, 0){\line(1, 0){2}}
\put(0, 0){\line(0, 1){2}}
\put(1, 2){\line(-1, 0){1}}
\put(2, 1){\line(0, -1){1}}
\put(1, 0){\line(0, 1){2}}
\put(0, 1){\line(1, 0){2}}
\end{picture}$ tako da svaka tromino-pločica prekriva točni tri polja ploče, a međusobno se ne prekrivaju.
Koliko je najmanje tromino-pločica potrebno postaviti na ploču ako želimo da se nakon toga više ne može postaviti nijedna dodatna tromino-pločica.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Odgovor je $11$
Kad bi bilo manje ili jednako $10$ to bi znaćilo da ima preko $34$ rupe podjeljeno u $16$ $2\times 2$ kvadratića znaći da barem u jednog stane $3$ tjst može se stavit još $1$.
Kombinaciju s $11$ tromino pločica postoji al to će morat ostat u povjerenju mene i čitatelja jer ne planiram objašnjavat konstrukciju.