Neocijenjeno
23. rujna 2023. 18:05 (2 godine, 4 mjeseci)
Ukrug je poredano konačno mnogo realnih brojeva. Svaki broj je obojan u crveno, bijelo ili plavo. Svaki crveni broj dvaput je manji od zbroja dvaju njemu susjednih brojeva, svaki bijeli broj jednak je zbroju dvaju njemu susjednih brojeva, a svaki plavi broj je dvaput veći od zbroja dvaju njemu susjednih brojeva. Neka je  zbroj svih bijelih brojeva, a
zbroj svih bijelih brojeva, a  zbroj svih plavih brojeva, pri čemu su oba zbroja različita od
zbroj svih plavih brojeva, pri čemu su oba zbroja različita od  .
.
Odredi omjer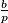 .
.
 zbroj svih bijelih brojeva, a
zbroj svih bijelih brojeva, a  zbroj svih plavih brojeva, pri čemu su oba zbroja različita od
zbroj svih plavih brojeva, pri čemu su oba zbroja različita od  .
.Odredi omjer
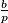 .
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
 Školjka
Školjka 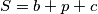 Očito. Sada također imamo
Očito. Sada također imamo 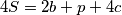 Zašto? Pa iz uvjeta zadatke
Zašto? Pa iz uvjeta zadatke 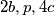 su dvostruki zbroj ljevog i desnog. I zato sto svaki broj ima i ljevog i desnog susjeda. Svaki broj cemo zbrojit
su dvostruki zbroj ljevog i desnog. I zato sto svaki broj ima i ljevog i desnog susjeda. Svaki broj cemo zbrojit  puta. Sad malo algebre i dobijemo
puta. Sad malo algebre i dobijemo