Neocijenjeno
23. rujna 2023. 18:57 (1 godina, 3 mjeseci)
Nađite sve funkcije
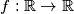
takve da je
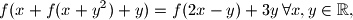
uz uvjet da je
injektivan.
%V0
Nađite sve funkcije $f : \mathbb{R} \rightarrow \mathbb{R}$ takve da je $$f(x+f(x+y^2)+y)=f(2x-y) + 3y \, \forall x, y \in \mathbb{R}\text{,}$$ uz uvjet da je $f$ injektivan.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kada uvrstimo y=0 dobijemo: f(x + f(x)) = f(2x) te iz f injekcija slijedi: x + f(x) = 2x tj. f(x) = x no to nije rješenje jednadžbe. Dakle ne postoji rješenje jednadžbe.
Kada uvrstimo y=0 dobijemo:
f(x + f(x)) = f(2x) te iz f injekcija slijedi:
x + f(x) = 2x tj. f(x) = x no to nije rješenje jednadžbe.
Dakle ne postoji rješenje jednadžbe.
Školjka