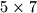
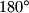
Na ploči dimenzija kojoj su sva polja bijela, potrebno je obojati točno polja crnom bojom tako da nastali raspored crnih i bijelih polja na ploči bude centralnosimetričan, tj. da se ne mijenja rotacijom za oko središta ploče. Na koliko je načina to moguće napraviti?
%V0
Na ploči dimenzija $5\times 7$ kojoj su sva polja bijela, potrebno je obojati točno $17$ polja crnom bojom tako da nastali raspored crnih i bijelih polja na ploči bude centralnosimetričan, tj. da se ne mijenja rotacijom za $180^\circ$ oko središta ploče. Na koliko je načina to moguće napraviti?
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Uoći da je središnje polje crno. Onda postoji 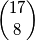naćina da odaberemo pola polja s jedne strane.
Uoći da je središnje polje crno. Onda postoji
$${17 \choose 8}$$ naćina da odaberemo pola polja s jedne strane.
Školjka 
kojoj su sva polja bijela, potrebno je obojati točno 
polja crnom bojom tako da nastali raspored crnih i bijelih polja na ploči bude centralnosimetričan, tj. da se ne mijenja rotacijom za 
oko središta ploče. Na koliko je načina to moguće napraviti? 
naćina da odaberemo pola polja s jedne strane.