Školjka
Tečajevi
MetaMath '24
Izbornik
Početna
Arhiva zadataka
Predavanja
Natjecanja
Tečajevi
Registracija
Prijava
Svi zadaci
Rješenja
Traži
Pomoć
O nama
Neocijenjeno
27. rujna 2023. 23:24 (1 godina, 2 mjeseci)
Korisnik:
Patrlk
Zadatak:
Općinsko natjecanje 2011 SŠ4 8
(Sakrij tekst zadatka)
Neka je
prirodan broj. Dokaži da je broj neparnih brojeva među brojevima
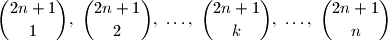
neparan.
%V0 Neka je $n$ prirodan broj. Dokaži da je broj neparnih brojeva među brojevima $$ {2n + 1 \choose 1}, \ {2n + 1 \choose 2}, \ \dots, \ {2n + 1 \choose k}, \ \dots, \ {2n + 1 \choose n} $$ neparan.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Tvrdnja je jednaka tome da dokažemo da je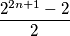
Neparan. Što je trivijalno.
Tvrdnja je jednaka tome da dokažemo da je $$\frac{2^{2n + 1} - 2}{2}$$ Neparan. Što je trivijalno.
Školjka 
prirodan broj. Dokaži da je broj neparnih brojeva među brojevima 
neparan. 
Neparan. Što je trivijalno.