Točno
7. listopada 2023. 22:42 (1 godina, 4 mjeseci)
Let
be an acute triangle with
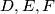
the feet of the altitudes lying on
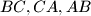
respectively. One of the intersection points of the line
and the circumcircle is
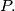
The lines
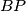
and
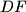
meet at point
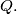
Prove that
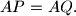
Proposed by Christopher Bradley, United Kingdom
%V0
Let $ABC$ be an acute triangle with $D, E, F$ the feet of the altitudes lying on $BC, CA, AB$ respectively. One of the intersection points of the line $EF$ and the circumcircle is $P.$ The lines $BP$ and $DF$ meet at point $Q.$ Prove that $AP = AQ.$
Proposed by Christopher Bradley, United Kingdom
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Četverokut $APBC$ je tetivan.
Što znaći da je $\angle APQ = \angle C$
Oznaćimo s $H$ ortocentar trokuta.
Tada je
$$\angle C = \angle EHA = \angle DHB$$
Sad odavde imamo da je
$$\angle HBC = \angle HAC = 90 - \angle C$$
Iz tetivnih četverokuta $AEHF$ i $FHDB$ imamo da je
$\angle EFD = 180 - 2\angle C$ i da je $\angle DFB = \angle C$. Iz toga da je $\angle AFP = \angle DFB$ imamo da je četverokut $AFPQ$ tetivan.
A sad iz $\angle C = \angle AFE = \angle PFB = \angle AQP$ slijedi tvrdnja zadatka.
| 3. rujna 2024. 16:34 | loki6 | Točno |
Školjka 
je tetivan. Što znaći da je 
ortocentar trokuta. Tada je 
Sad odavde imamo da je 
i 
imamo da je 
i da je 
. Iz toga da je 
imamo da je četverokut 
tetivan.
slijedi tvrdnja zadatka.