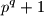
Odredi sve proste brojeve i takve da je također prost.
%V0
Odredi sve proste brojeve $p$ i $q$ takve da je $\displaystyle p^q+1$ također prost.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Ako je neparan, je paran, sto je nemoguce. Dakle .
ako je neparan, daje pri djeljenju s , sto bi znacilo da daje odnosno , sto je nemoguce.
Onda mora biti paran, odnosno
$p^q+1=r$
Ako je $p$ neparan, $r$ je paran, sto je nemoguce. Dakle $p=2$.
$2^q+1=r$
ako je $q$ neparan, daje $2$ pri djeljenju s $3$, sto bi znacilo da $r$ daje $0$ odnosno $r=3$, sto je nemoguce.
Onda $q$ mora biti paran, odnosno $q=2$
$$(p,q,r)=(2,2,3)$$
Školjka 
i 
takve da je 
također prost. 
Ako je 
je paran, sto je nemoguce. Dakle 
.
pri djeljenju s 
, sto bi znacilo da 
odnosno 
, sto je nemoguce.
