Poznato je da, ako polinom ima realne koeficijente, ako je  njegova nultočka, onda je
njegova nultočka, onda je 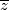 također njegova nultočka.
također njegova nultočka.
Kako je dani polinom trećeg stupnja slijedi da je barem jedna njegova nultočka realna, neka je ta nultočka  , a ostale dvije
, a ostale dvije  i
i  .
.
Znamo da vrijedi 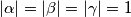 pa slijedi
pa slijedi 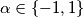 Budući da
Budući da 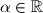 .
.
Pretpostavimo sada da 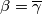 , onda slijedi da
, onda slijedi da 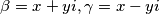 za
za 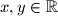 . Imamo dva slućaja:
. Imamo dva slućaja:
1) 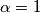
Iz 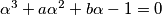 slijedi
slijedi 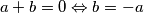 . Uvrštavajući slijedi:
. Uvrštavajući slijedi:
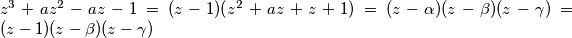
Pa: 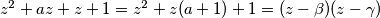 . Sada treba pronaći sve
. Sada treba pronaći sve  takve da su nultočke te kvadratne jednadžbe međusobno kompleksno konjugirani brojevi, a to se događa ako je
takve da su nultočke te kvadratne jednadžbe međusobno kompleksno konjugirani brojevi, a to se događa ako je ![D=(a+1)^2-4\cdot1\cdot1 \le 0 \Leftrightarrow a \in [-3, 1]](/media/m/1/e/6/1e6ee5c32956e5db99ae31458907b2bd.png) . Onda za te nultočke vrijedi Iz Vieteovih formula
. Onda za te nultočke vrijedi Iz Vieteovih formula 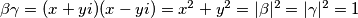 pa smo gotovi.
pa smo gotovi.
2) 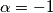
Iz 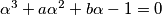 slijedi
slijedi 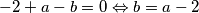 . Uvrštavajući slijedi:
. Uvrštavajući slijedi:
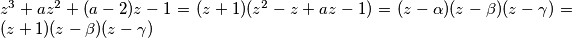
Pa 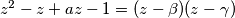 , ali, iz Vieteovih formula slijedi:
, ali, iz Vieteovih formula slijedi: 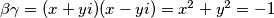 Što nije moguće jer
Što nije moguće jer 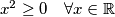
Sada, ako su dvije nultočke danog polinoma realne, onda je nužno i treća.
Pogledajmo sada slućaj kada 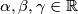
onda vrijedi: 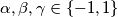 , ali po Diricheltovom prinicpu slijedi da su neka dva među
, ali po Diricheltovom prinicpu slijedi da su neka dva među 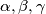 jednaki, tj. budući da su realni, onda su i međusobno kompleksno konjugirani, te već imamo pokriven taj slućaj.
jednaki, tj. budući da su realni, onda su i međusobno kompleksno konjugirani, te već imamo pokriven taj slućaj.
Odgovor: svi ![a \in [-3, -1]](/media/m/6/a/1/6a1576d4b4883b82d247f9baa8b94376.png) i
i 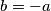
Poznato je da, ako polinom ima realne koeficijente, ako je $z$ njegova nultočka, onda je $\overline{z}$ također njegova nultočka. \\
Kako je dani polinom trećeg stupnja slijedi da je barem jedna njegova nultočka realna, neka je ta nultočka $\alpha$, a ostale dvije $\beta$ i $\gamma$. \\
Znamo da vrijedi $|\alpha| = |\beta| = |\gamma|=1$ pa slijedi $\alpha \in \{ -1, 1\}$ Budući da $\alpha \in \mathbb{R}$. \\
Pretpostavimo sada da $\beta = \overline{\gamma}$, onda slijedi da $\beta = x+yi, \gamma = x-yi$ za $x, y \in \mathbb{R}$. Imamo dva slućaja: \\
1) $\alpha=1$ \\
Iz $\alpha^3 + a\alpha^2+b\alpha-1=0$ slijedi $a+b=0 \Leftrightarrow b=-a$. Uvrštavajući slijedi: \\
$z^3 + az^2 - az - 1 = (z-1)(z^2+az+z+1) = (z-\alpha)(z-\beta)(z-\gamma) = (z-1)(z-\beta)(z-\gamma)$\\ Pa:
$z^2 + az+z+1=z^2 + z(a+1)+1= (z-\beta)(z-\gamma)$. Sada treba pronaći sve $a$ takve da su nultočke te kvadratne jednadžbe međusobno kompleksno konjugirani brojevi, a to se događa ako je $D=(a+1)^2-4\cdot1\cdot1 \le 0 \Leftrightarrow a \in [-3, 1]$. Onda za te nultočke vrijedi Iz Vieteovih formula $\beta\gamma = (x+yi)(x-yi)=x^2+y^2=|\beta|^2=|\gamma|^2=1$ pa smo gotovi.
2) $\alpha=-1$ \\
Iz $\alpha^3 + a\alpha^2+b\alpha-1=0$ slijedi $-2+a-b=0 \Leftrightarrow b=a-2$. Uvrštavajući slijedi: \\
$z^3 + az^2 + (a-2)z - 1 = (z+1)(z^2-z+az-1) = (z-\alpha)(z-\beta)(z-\gamma) = (z+1)(z-\beta)(z-\gamma)$ \\
Pa $z^2-z+az-1=(z-\beta)(z-\gamma)$, ali, iz Vieteovih formula slijedi: $\beta\gamma = (x+yi)(x-yi)=x^2+y^2=-1$ Što nije moguće jer $x^2 \ge 0 \quad \forall x \in \mathbb{R}$
Sada, ako su dvije nultočke danog polinoma realne, onda je nužno i treća.\\
Pogledajmo sada slućaj kada $\alpha, \beta, \gamma \in \mathbb{R}$\\
onda vrijedi: $\alpha, \beta, \gamma \in \{-1, 1 \}$, ali po Diricheltovom prinicpu slijedi da su neka dva među $\alpha, \beta, \gamma$ jednaki, tj. budući da su realni, onda su i međusobno kompleksno konjugirani, te već imamo pokriven taj slućaj. \\
Odgovor: svi $a \in [-3, -1]$ i $b=-a$
 njegova nultočka, onda je
njegova nultočka, onda je 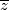 također njegova nultočka.
također njegova nultočka.  , a ostale dvije
, a ostale dvije  i
i  .
. 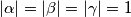 pa slijedi
pa slijedi 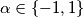 Budući da
Budući da 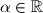 .
. 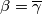 , onda slijedi da
, onda slijedi da 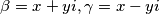 za
za 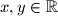 . Imamo dva slućaja:
. Imamo dva slućaja: 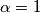
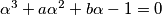 slijedi
slijedi 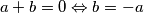 . Uvrštavajući slijedi:
. Uvrštavajući slijedi: 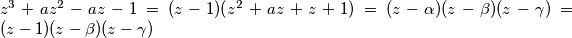
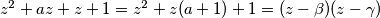 . Sada treba pronaći sve
. Sada treba pronaći sve  takve da su nultočke te kvadratne jednadžbe međusobno kompleksno konjugirani brojevi, a to se događa ako je
takve da su nultočke te kvadratne jednadžbe međusobno kompleksno konjugirani brojevi, a to se događa ako je ![D=(a+1)^2-4\cdot1\cdot1 \le 0 \Leftrightarrow a \in [-3, 1]](/media/m/1/e/6/1e6ee5c32956e5db99ae31458907b2bd.png) . Onda za te nultočke vrijedi Iz Vieteovih formula
. Onda za te nultočke vrijedi Iz Vieteovih formula 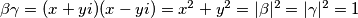 pa smo gotovi.
pa smo gotovi.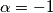
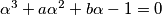 slijedi
slijedi 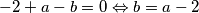 . Uvrštavajući slijedi:
. Uvrštavajući slijedi: 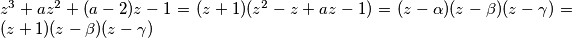
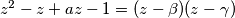 , ali, iz Vieteovih formula slijedi:
, ali, iz Vieteovih formula slijedi: 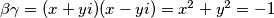 Što nije moguće jer
Što nije moguće jer 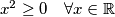
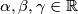
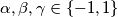 , ali po Diricheltovom prinicpu slijedi da su neka dva među
, ali po Diricheltovom prinicpu slijedi da su neka dva među 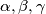 jednaki, tj. budući da su realni, onda su i međusobno kompleksno konjugirani, te već imamo pokriven taj slućaj.
jednaki, tj. budući da su realni, onda su i međusobno kompleksno konjugirani, te već imamo pokriven taj slućaj. ![a \in [-3, -1]](/media/m/6/a/1/6a1576d4b4883b82d247f9baa8b94376.png) i
i 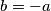
 Školjka
Školjka  su moduli svih korijena jednadžbe
su moduli svih korijena jednadžbe 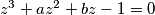 jednaki
jednaki  ?
?