u slucaju 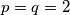 , imamo
, imamo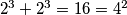 , pa je
, pa je 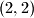 ok par.
ok par.
(1.)
pretp. da su 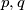 neparni. Tada je
neparni. Tada je 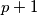 paran.
paran. 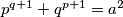
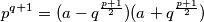
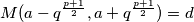
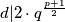 .
.  nije
nije  jer bi tada
jer bi tada  bio paran. ako je
bio paran. ako je 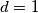 imamo:
imamo: 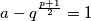
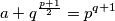
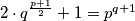
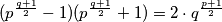 , no ovo nema rjesenja zato jer su oba dva faktora na lijevoj strani djeljivi sa
, no ovo nema rjesenja zato jer su oba dva faktora na lijevoj strani djeljivi sa  , pa je lijeva strana dijelijva sa
, pa je lijeva strana dijelijva sa  , sto bi znacilo da
, sto bi znacilo da 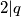 sto je prema pretpostavci nemoguce.
sto je prema pretpostavci nemoguce.
ako je 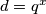 ,
, 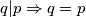
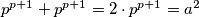 , ako
, ako 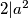 , tada
, tada 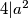 , pa onda
, pa onda 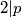 , sto je nemoguce prema pretpostavci. Dakle,
, sto je nemoguce prema pretpostavci. Dakle, 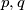 nemogu istovremeno biti neparni.
nemogu istovremeno biti neparni.
(2.)
Pretp. da je barem jedan broj paran. WLOG 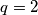 .
.
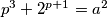 ,
,  je neparan pa je
je neparan pa je 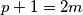
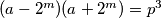 .
.
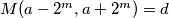 ,
, 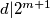 , ako
, ako 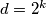 ,
, 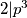 sto je nemoguce. Preostaje
sto je nemoguce. Preostaje 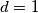 .
.
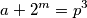
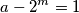
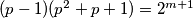
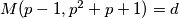 ,
, 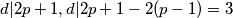
Ocito 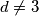 , mora biti
, mora biti 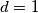 , sto nam kaze da je
, sto nam kaze da je 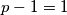 , odnosno
, odnosno 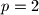 , sto nemoze biti zbog pretpostavke.
, sto nemoze biti zbog pretpostavke.
Dakle jedino rjesenje je 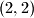
u slucaju $p=q=2$, imamo$2^3+2^3=16=4^2$, pa je $(2,2)$ ok par.
(1.)
pretp. da su $p,q$ neparni. Tada je $p+1$ paran.
$p^{q+1}+q^{p+1}=a^2$
$$p^{q+1}=(a-q^{\frac{p+1}{2}})(a+q^{\frac{p+1}{2}})$$
$M(a-q^{\frac{p+1}{2}},a+q^{\frac{p+1}{2}})=d$
$d|2\cdot q^\frac{p+1}{2}$. $d$ nije $2$ jer bi tada $p$ bio paran. ako je $d=1$ imamo:
$$a-q^{\frac{p+1}{2}}=1$$
$$a+q^{\frac{p+1}{2}}=p^{q+1}$$
$2\cdot q^{\frac{p+1}{2}}+1=p^{q+1}$
$(p^{\frac{q+1}{2}}-1)(p^{\frac{q+1}{2}}+1)=2\cdot q^{\frac{p+1}{2}}$, no ovo nema rjesenja zato jer su oba dva faktora na lijevoj strani djeljivi sa $2$, pa je lijeva strana dijelijva sa $4$, sto bi znacilo da $2|q$ sto je prema pretpostavci nemoguce.
ako je $d=q^x$, $q|p\Rightarrow q=p$
$p^{p+1}+p^{p+1}=2\cdot p^{p+1}=a^2$, ako $2|a^2$, tada $4|a^2$, pa onda $2|p$, sto je nemoguce prema pretpostavci. Dakle, $p,q$ nemogu istovremeno biti neparni.
(2.)
Pretp. da je barem jedan broj paran. WLOG $q=2$.
$p^3+2^{p+1}=a^2$, $p$ je neparan pa je $p+1=2m$
$(a-2^m)(a+2^m)=p^3$.
$M(a-2^m,a+2^m)=d$, $d|2^{m+1}$, ako $d=2^k$, $2|p^3$ sto je nemoguce. Preostaje $d=1$.
$$a+2^m=p^3$$
$$a-2^m=1$$
$(p-1)(p^2+p+1)=2^{m+1}$
$M(p-1,p^2+p+1)=d$, $d|2p+1,d|2p+1-2(p-1)=3$
Ocito $d\neq 3$, mora biti $d=1$, sto nam kaze da je $p-1=1$, odnosno $p=2$, sto nemoze biti zbog pretpostavke.
Dakle jedino rjesenje je $(2,2)$
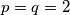 , imamo
, imamo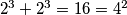 , pa je
, pa je 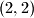 ok par.
ok par.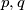 neparni. Tada je
neparni. Tada je 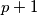 paran.
paran. 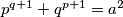
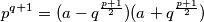
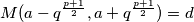
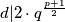 .
.  nije
nije  jer bi tada
jer bi tada  bio paran. ako je
bio paran. ako je 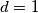 imamo:
imamo: 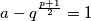
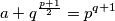
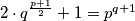
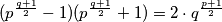 , no ovo nema rjesenja zato jer su oba dva faktora na lijevoj strani djeljivi sa
, no ovo nema rjesenja zato jer su oba dva faktora na lijevoj strani djeljivi sa  , pa je lijeva strana dijelijva sa
, pa je lijeva strana dijelijva sa  , sto bi znacilo da
, sto bi znacilo da 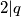 sto je prema pretpostavci nemoguce.
sto je prema pretpostavci nemoguce.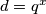 ,
, 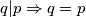
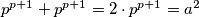 , ako
, ako 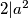 , tada
, tada 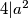 , pa onda
, pa onda 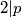 , sto je nemoguce prema pretpostavci. Dakle,
, sto je nemoguce prema pretpostavci. Dakle, 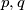 nemogu istovremeno biti neparni.
nemogu istovremeno biti neparni.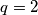 .
.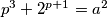 ,
,  je neparan pa je
je neparan pa je 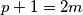
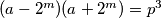 .
.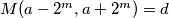 ,
, 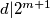 , ako
, ako 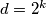 ,
, 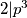 sto je nemoguce. Preostaje
sto je nemoguce. Preostaje 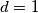 .
.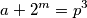
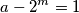
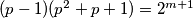
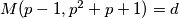 ,
, 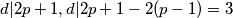
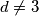 , mora biti
, mora biti 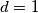 , sto nam kaze da je
, sto nam kaze da je 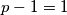 , odnosno
, odnosno 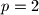 , sto nemoze biti zbog pretpostavke.
, sto nemoze biti zbog pretpostavke.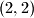
 Školjka
Školjka 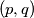 prostih brojeva za koje je broj
prostih brojeva za koje je broj 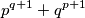 potpuni kvadrat.
potpuni kvadrat.