Neocijenjeno
26. listopada 2023. 15:03 (1 godina, 4 mjeseci)
Duljine stranica trokuta su
,
i
, a
je duljina polumjera opisane mu kružnice. Odredite kutove trokuta ako vrijedi
.
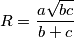
%V0
Duljine stranica trokuta su $a$, $b$ i $c$, a $R$ je duljina polumjera opisane mu kružnice. Odredite kutove trokuta ako vrijedi $R = \displaystyle \frac{a\sqrt{bc}}{b+c}$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Fora zadatak.
Prisjetimo se :
\[b + c \geq 2\sqrt{bc}\]
Iz toga imamo :
\begin{align*}
\frac{b + c}{\sqrt{bc}} &\geq 2 \\
\frac{\sqrt{bc}}{b + c} &\leq \frac{1}{2}
\end{align*}
Tojest
\[R = \frac{a\sqrt{bc}}{b + c} \leq \frac{a}{2}\]
Trivijalno je da je $R \geq \frac{a}{2}$ što implicira $R = a$ , $b = c$.
Time dobivamo kutove $45$ , $45$ , $90$
Školjka 
Iz toga imamo : 
što implicira 
, 
.
, 