Neocijenjeno
29. listopada 2023. 15:58 (2 godine, 3 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Općenito neka je 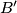 reflekcija od
reflekcija od  preko
preko  . Trokuti
. Trokuti 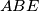 i
i 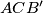 su slićni. Točnije trokut
su slićni. Točnije trokut 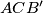 je homotetija trokuta
je homotetija trokuta 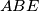 s obzirom na točku
s obzirom na točku  i s omjerom
i s omjerom  .
.
Tvrdnja zadatka je ekvivalentna da dokažemo :
 je težište
je težište 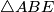 ako i samo ako je
ako i samo ako je  težište
težište 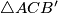
Točnije 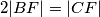 očito implicira da je
očito implicira da je  težište trokuta
težište trokuta 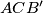
Dok kolinearnost  ,
,  ,
,  implicira da
implicira da 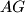 sijeće sjećište dijagonala pravokutnika
sijeće sjećište dijagonala pravokutnika 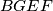 tojest polovište stranice
tojest polovište stranice  i iz toga imamo da je
i iz toga imamo da je  sjećište dvije težišnice tjst da je ono tešište.
sjećište dvije težišnice tjst da je ono tešište.
Ako je  težište i
težište i 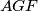 su kolinearni onda je
su kolinearni onda je  sjećište
sjećište  težišta. Točnije
težišta. Točnije  je homotetija točke
je homotetija točke  s obzirom na
s obzirom na  s omjerom
s omjerom  što znaći da je
što znaći da je  isto težište. (To vidimo iz slićnosti
isto težište. (To vidimo iz slićnosti 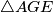 i
i 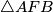
Ako je  težište onda oznaćimo težište trokuta
težište onda oznaćimo težište trokuta 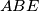 s
s 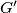 iz homotetije / slićnosti vrjedi da je
iz homotetije / slićnosti vrjedi da je 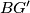 okomica na
okomica na  tojest
tojest 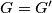 i
i  je težište
je težište 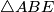
Komentari:
Patrlk, 29. listopada 2023. 16:03
 Školjka
Školjka  s tupim kutom kod vrha
s tupim kutom kod vrha  i
i  polovišta stranica
polovišta stranica  i
i  redom,
redom,  takva da je
takva da je 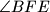 pravi, te
pravi, te 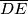 takva da je kut
takva da je kut 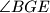 pravi.
pravi.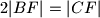 .
.