Školjka Točno
31. listopada 2023. 16:32 (6 mjeseci)
Prijateljice Anica i Neda igraju igru tako da u svakom potezu, nakon što jedna od njih kaže broj 
, druga mora reći neki broj oblika 
pri čemu su 
i 
prirodni brojevi za koje vrijedi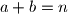 
. Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj 
?
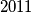, druga mora reći neki broj oblika pri čemu su i prirodni brojevi za koje vrijedi 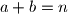. Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj 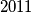? Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Za svaki broj n>4 možemo sljedećom transformacijom doći do broja n-1: n=(n-1)+1=>(n-1)×1=n-1 To znači da svaki početni broj veći ili jednak 5 možemo smanjivati za jedan sve dok n ne bude jednak 5. Tada primjenimo sljedeće transformacije: 5=2+3=>2×3=6=3+3=>3×3=9=6+3=>6×3=18 18=17+1=>17×1=17=11+6=>11×6=66 66=42+24=>42×24=1008 1008=1006+2=>1006×2=2012 2012=2011+1=>2011×1=2011 Dakle, za sve je početne brojeve veće ili jednake 5 moguće nakon određenog vremena da je neka od njih rekla broj 2011. Preostaje dokazati da za brojeve manje od 5 to nije moguće. Četiri možemo rastaviti na 2+2 ili 1+3 od čega niti jedan rastav ne dava broj veći od početnoga broj. To vrijedi i za 3=1+2 i za 2=1+1.