Točno
31. listopada 2023. 21:21 (2 godine, 4 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
14+8z je kongurentno 2 (mod 4) pa je onda x^2+y^2 isto kongurentno 2 (mod 4) što znači da su x i y neparni. Kvadrati neparnih brojeva uvijek daju ostatak 1 pri dijeljenju s 8: (2n+1)^2=4n^2+4n+1=4n(n+1)+1, n i n+1 su dva uzastopna broja pa je jedan od njih sigurno djeljiv s 2 pa i time 4n(n+1) djeljiv s 8. Zbog toga je x^2+y^2 kongurentno 2 (mod 8) dok je 14+8z kongurentno 6 (mod 8) što je kontradikcija pa zato ta jednadžba nema cjelobrojnih rješenja.
 Školjka
Školjka 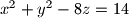 cjelobrojnih rješenja? Ako ima, odredi ih. Ako nema, dokaži.
cjelobrojnih rješenja? Ako ima, odredi ih. Ako nema, dokaži.