Školjka

2y^2-75y+5 je kongurentno 2y^2 (mod 5) pa je x^2 je kongurentno 2y^2 (mod 5). Kvadrat cijelog broja je kongurentan -1,0 ili 1 (mod 5) pa da bi izrazi 2y^2 i x^2bili kongurentni oba izraza moraju biti kongurentni 0 (mod 5) odnosno x^2 i 2y^2 su djeljivi s 5 što znači da su i x i y djeljivi s 5. 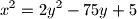Ako uvrstimo x=5a i y=5b gdje su a i b cijeli brojevi, te jednadžbu podijelimo s 5 dobijemo: 5a^2=b^2-75b+1 Kako je lijeva strana jednadžbe očito djeljiva s 5 dok druga očito nije, dolazimo do kontradikcije pa zato zadana jednadžba nema cjelobrojnih rješenja.