Neocijenjeno
6. studenoga 2023. 22:37 (1 godina, 4 mjeseci)
Odredi sve parove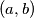 
prirodnih brojeva za koje vrijedi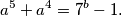 
Odredi sve parove $(a, b)$ prirodnih brojeva za koje vrijedi
\[ a^5 + a^4 = 7^b - 1 \text. \]
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
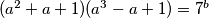
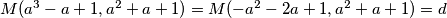
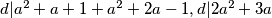
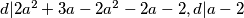
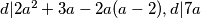
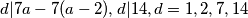
zbog parnosti oba dviju strana,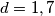 
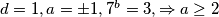
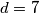
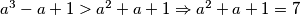
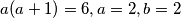
Jedino rješenje je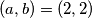 
$(a^2+a+1)(a^3-a+1)=7^b$
$M(a^3-a+1,a^2+a+1)=M(-a^2-2a+1,a^2+a+1)=d$
$d|a^2+a+1+a^2+2a-1, d|2a^2+3a$
$d|2a^2+3a-2a^2-2a-2,d|a-2$
$d|2a^2+3a-2a(a-2),d|7a$
$d|7a-7(a-2),d|14, d=1,2,7,14$
zbog parnosti oba dviju strana, $d=1,7$
$d=1,a= \pm 1, 7^b=3, \Rightarrow a \ge 2$
$d=7$
$a^3-a+1>a^2+a+1 \Rightarrow a^2+a+1=7$
$a(a+1)=6, a=2,b=2$
Jedino rješenje je $(a,b)=(2,2)$
Školjka