Kliknite ovdje kako biste prikazali rješenje.
Znamo da je ukupni volumen stošca isti u oba položaja pa možemo to iskoristiti.
Cilj je sada dobiti sustav jednadžbi iz kojeg bih mogao izvući h.
Ne znam ništa o površinama baza osim o njihovim odnosima, a i čini mi se nespretno baviti njima zbog odnosa koji su dani u zadatku.
Ono što mi najbolje obuhvaća sve uvjete su pojedini volumeni vode i praznina u posudi.
Ukupni volumen V mogu predstaviti na dva načina: preko prvog i drugog slučaja.
Znam da su dvije stvari konstante:
Ukupni volumen posude i volumen vode.
Stožac koji stvara praznina u prvom slučaju i krnji stožac koji ta ista praznina stvara u drugom slučaju jednakih su volumena.
V_praznina=V∙〖k_2〗^3 V_praznina=V∙(1-(k_1)^3)
V∙〖k_2〗^3= V∙(1-(k_1)^3)
〖k_2〗^3= V∙(1-(k_1)^3)
Konstante k1 i k2 mogu dobiti preko postavljenih uvjeta
k1 = 8/h
k2 = (h-2)/h
Uvrstivši ovo u izraz dobivam jednadžbu s jednom nepoznanicom:
(8^3) / (h^3) = 1 - ((h-2)^3) / (h^3)
Sređivanjem dolazim do kvadratne jednadžbe:
6(h^2) - 12h - 504 = 0
Dajući rješenja 1 + 85^(1/2) i 1 - 85^(1/2)
Prvo je rješenje moguće jer se poklapa s uvjetima: h > 8 i h > 2
Drugo rješenje je samo po sebi negativno te stoga nije rješenje ove situacije.
 Školjka
Školjka 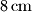 ispod vrha stošca. Ako stožac preokrenemo, razina vode je
ispod vrha stošca. Ako stožac preokrenemo, razina vode je 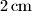 ispod osnovke stošca.
ispod osnovke stošca.