Točno
26. studenoga 2023. 19:15 (2 godine, 3 mjeseci)
Dokaži da ako su brojevi

i
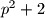
prosti, onda je i
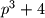
prost.
%V0
Dokaži da ako su brojevi $p$ i $p^2+2$ prosti, onda je i $p^3 +4$ prost.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
p^2+2=p^2-1+3=(p-1)(p+1)+3 je djeljivo s 3 za svaki p>3 ili p=2 pa onda izraz nije prost što znači da je p=3 iz čega slijedi da je p^3+4 jednako 29 što je također prost broj.
p^2+2=p^2-1+3=(p-1)(p+1)+3 je djeljivo s 3 za svaki p>3 ili p=2 pa onda izraz nije prost što znači da je p=3 iz čega slijedi da je p^3+4 jednako 29 što je također prost broj.