Školjka

Odmah uočimo da je moguća kombinacija 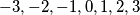$-3,-2,-1,0,1,2,3$. Pokažimo da nije moguće imati više od 3 pozitivna / negativna broja u skupu. Riješimo pozitivan slučaj, negativan je kompletno analogan. Promatrajmo 4 pozitivna broja 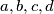$a,b,c,d$, s tim da 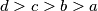$d>c>b>a$. Primijetimo da nikada nećemo dobiti da je suma bilo kojeg para od tih 4 brojeva jednaka a ili b. Također, primijetimo da u bilo kojoj promatranoj trojci, za par brojeva koji ćemo sumirati nikada nećemo uzimati d jer je najveći, tj. 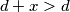$d+x>d$. Dakle imamo moguće trojke: 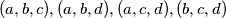$(a,b,c),(a,b,d),(a,c,d),(b,c,d)$. 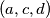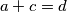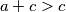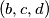Iz $(a,c,d)$ mora vrijediti da $a+c=d$ (jer je $a+c>c$, a jedino je $d>c$), a iz $(b,c,d)$ isto tako mora vrijediti da 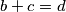$b+c=d$ (jer je 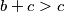$b+c>c$, a jedino je $d>c$). Dobicamo da $d=b+c>a+c=d$. 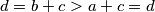Netočna tvrdnja, dakle nemoguće je da imamo 4 pozitivna cijela broja, tj. nemoguće je imati 4 negativna broja. Dakle najviše moguće brojeva u skupu je 7.