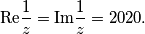Neocijenjeno
10. prosinca 2023. 14:42 (2 godine, 3 mjeseci)
Odredi argument kompleksnog broja  ako vrijedi
ako vrijedi 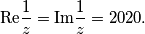
Odredi argument kompleksnog broja $z$ ako vrijedi
\[\text{Re} \frac{1}{z} = \text{Im} \frac{1}{z} = 2020.\]
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je $z$ kompleksni broj oblika $z = x + yi$, odnosno u trigonometrijskom obliku: $z = r(\cos \phi + i \sin \phi )$.\\
Odredimo prvo "sredimo" izraz $\frac{1}{z}$:\\
$$\frac{1}{x+yi} = \frac{1}{x+yi} \cdot \frac{x-yi}{x-yi} = \frac{x-yi}{{x}^{2}+{y}^{2}}= \frac{x}{{x}^{2}+{y}^{2}} + i \cdot \frac{-y}{{x}^{2}+{y}^{2}}$$
Sada proizlazi:
$$(1) \operatorname{Re}{\frac{1}{z}} = \frac{x}{{x}^{2}+{y}^{2}} = 2020,$$
$$(2) \operatorname{Im}{\frac{1}{z}} = \frac{-y}{{x}^{2}+{y}^{2}} = 2020.$$
Dijeljenjem druge jednadžbe s prvom, dobijemo:
$$ \frac{y}{x}=\frac{-2020}{2020} = -1 \Rightarrow \tg \phi = -1 \Rightarrow \phi = \frac{3\pi}{4} + k\pi, k\in \mathbb{Z}$$
Naime, argument nekog kompleksnog broja nalazi se u intervalu $[0, 2\pi\rangle$ iz čega proizlazi da je $ \phi \in \{ \frac{3\pi}{4}, \frac{7\pi}{4}\}$.\\
Ujedno vrijedi i $x = r\cos\phi$ i $y = r\sin\phi$ te se jednadžbe $(1)$ i $(2)$ mogu zapisati u obliku: \\
$$(1) \operatorname{Re}{\frac{1}{z}} = \frac{r\cos\phi}{{(r\cos\phi)}^{2}+{(r\sin\phi)}^{2}} = \frac{r\cos\phi}{{r}^{2}} = \frac{\cos\phi}{{r}} = 2020,$$
$$(2) \operatorname{Im}{\frac{1}{z}} = \frac{-r\sin\phi}{{(r\cos\phi)}^{2}+{(r\sin\phi)}^{2}} = \frac{-r\sin\phi}{{r}^{2}} = \frac{-\sin\phi}{{r}} = 2020.$$
Budući da je $r > 0$, slijedi: $\frac{\cos\phi}{2020} > 0$ i $\frac{-\sin\phi}{2020} > 0$, tj.: \\
$$\cos\phi > 0,$$
$$\sin\phi < 0.$$
Naime, ovaj sustav nejednadžbe ne vrijedi za $\phi = \frac{3\pi}{4}$ što znači da je jedino rješenje: $\phi = \frac{7\pi}{4}$.\\
NAPOMENA: Prilikom kraćenja razlomaka pri dijeljenju jednadžbi (sa ${x}^{2}+{y}^{2}$ i $r$) treba pisati uvjet da su ti izrazi različiti od nule. Međutim, to nije potrebno zato što na početku zadatka mora vrijediti $z \neq 0$ iz čega slijedi svi nenapisani uvjeti.
 kompleksni broj oblika
kompleksni broj oblika 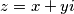 , odnosno u trigonometrijskom obliku:
, odnosno u trigonometrijskom obliku: 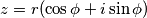 .
. :
: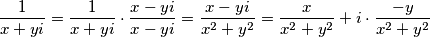 Sada proizlazi:
Sada proizlazi: 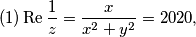
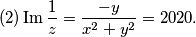 Dijeljenjem druge jednadžbe s prvom, dobijemo:
Dijeljenjem druge jednadžbe s prvom, dobijemo: 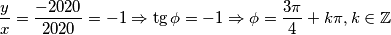 Naime, argument nekog kompleksnog broja nalazi se u intervalu
Naime, argument nekog kompleksnog broja nalazi se u intervalu 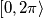 iz čega proizlazi da je
iz čega proizlazi da je 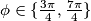 .
.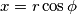 i
i 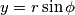 te se jednadžbe
te se jednadžbe  i
i  mogu zapisati u obliku:
mogu zapisati u obliku: 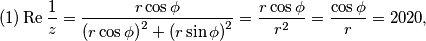
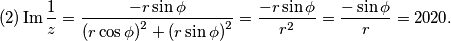 Budući da je
Budući da je 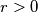 , slijedi:
, slijedi: 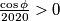 i
i 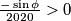 , tj.:
, tj.: 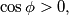
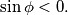 Naime, ovaj sustav nejednadžbe ne vrijedi za
Naime, ovaj sustav nejednadžbe ne vrijedi za 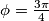 što znači da je jedino rješenje:
što znači da je jedino rješenje: 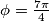 .
.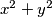 i
i  ) treba pisati uvjet da su ti izrazi različiti od nule. Međutim, to nije potrebno zato što na početku zadatka mora vrijediti
) treba pisati uvjet da su ti izrazi različiti od nule. Međutim, to nije potrebno zato što na početku zadatka mora vrijediti 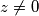 iz čega slijedi svi nenapisani uvjeti.
iz čega slijedi svi nenapisani uvjeti.  Školjka
Školjka