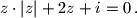Neocijenjeno
11. prosinca 2023. 18:36 (2 godine, 2 mjeseci)
Odredi sve kompleksne brojeve

za koje vrijedi
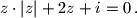
%V0
Odredi sve kompleksne brojeve $z$ za koje vrijedi $$
z\cdot |z|+2z+i=0\,.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je $z$ kompleksni broj oblika $z = x+yi, x,y \in \mathbb{R}$. Ovakve jednadžbe se rješavaju koristeći jednakosti kompleksnih brojeva, odnosno: $z_{1} = z_{2}$ ako i samo ako je $\operatorname{Re} (z_{1}) = \operatorname{Re} (z_{2})$ i $\operatorname{Im} (z_{1}) = \operatorname{Im} (z_{2})$.\\
Sredimo početnu jednadžbu:
$$(x+yi) \cdot \sqrt{x^{2}+y^{2}} + 2(x+yi) + i = 0$$
$$x \cdot \sqrt{x^{2}+y^{2}} +yi \cdot \sqrt{x^{2}+y^{2}} + 2x+2yi + i = 0$$
Grupirajmo realni i imaginarni dio izraza. Pritom se prisjetimo da je apsolutna vrijednost kompleksnog broja realan broj.
$$x \sqrt{x^{2}+y^{2}} +2x + 2yi + i +yi \cdot \sqrt{x^{2}+y^{2}} = 0$$
$$x \sqrt{x^{2}+y^{2}} +2x + i (2y + 1 + y\sqrt{x^{2}+y^{2}}) = 0$$
Bilo koji realni broj možemo prikazati kao kompleksni broj s imaginarnim dijelom jednakim nuli. Dakle, nulu možemo zapisati u obliku: $0 = 0 + 0i$.
$$x \sqrt{x^{2}+y^{2}} +2x + i (2y + 1 + y\sqrt{x^{2}+y^{2}}) = 0 + 0i$$
Iz jednakosti kompleksnih brojeva, dobijemo dvije jednadžbe koje čine sustav:
$$x \sqrt{x^{2}+y^{2}} +2x = 0,$$
$$2y + 1 + y\sqrt{x^{2}+y^{2}} = 0.$$
Sredimo prvu jednadžbu:
$$x(\sqrt{x^{2}+y^{2}} + 2) = 0,$$
iz čega proizlazi da je $x=0$ ili $\sqrt{x^{2}+y^{2}} + 2 = 0$. Valja primijeti kako drugi slučaj nema smisla jer se dobije $\sqrt{x^{2}+y^{2}} = -2$, a vrijednost korijena ne može biti negativan broj. Zapišimo matematičkim rječnikom: $\sqrt{x^{2}+y^{2}} \geq 0, \forall x,y \in \mathbb{R}$. Dakle, jedan i jedini uvjet je $x=0$. Uvrstimo to u drugu jednadžbu:
$$2y + 1 + y\sqrt{0+y^{2}} = 0$$
$$2y + 1 + y\sqrt{y^{2}} = 0$$
$$2y + 1 + y|y| = 0$$
1. slučaj: ako je $y < 0$.
$$2y + 1 + y(-y) = 0$$
$$y^{2} - 2y - 1= 0 \Rightarrow y = 1 \pm \sqrt{2}.$$
Pazimo da smo promatrali $y < 0$, tj. jedino rješenje ove jednadžbe je broj: $y = 1 - \sqrt{2}$.\\
2. slučaj: ako je $y \geq 0$.
$$2y + 1 + y(y) = 0$$
$$y^{2} + 2y + 1= 0 \Rightarrow y = -1.$$
Pazimo da smo promatrali $y \geq 0$, tj. ovaj slučaj nema rješenja: $y \in \emptyset.$\\
Dakle, jedino rješenje ove jednadžbe jest $z = i(1-\sqrt{2})$.
 kompleksni broj oblika
kompleksni broj oblika 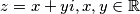 . Ovakve jednadžbe se rješavaju koristeći jednakosti kompleksnih brojeva, odnosno:
. Ovakve jednadžbe se rješavaju koristeći jednakosti kompleksnih brojeva, odnosno: 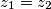 ako i samo ako je
ako i samo ako je 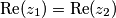 i
i 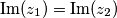 .
.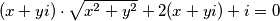
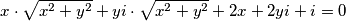 Grupirajmo realni i imaginarni dio izraza. Pritom se prisjetimo da je apsolutna vrijednost kompleksnog broja realan broj.
Grupirajmo realni i imaginarni dio izraza. Pritom se prisjetimo da je apsolutna vrijednost kompleksnog broja realan broj. 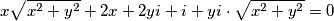
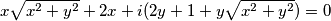 Bilo koji realni broj možemo prikazati kao kompleksni broj s imaginarnim dijelom jednakim nuli. Dakle, nulu možemo zapisati u obliku:
Bilo koji realni broj možemo prikazati kao kompleksni broj s imaginarnim dijelom jednakim nuli. Dakle, nulu možemo zapisati u obliku: 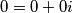 .
. 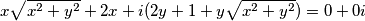 Iz jednakosti kompleksnih brojeva, dobijemo dvije jednadžbe koje čine sustav:
Iz jednakosti kompleksnih brojeva, dobijemo dvije jednadžbe koje čine sustav: 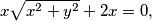
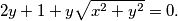 Sredimo prvu jednadžbu:
Sredimo prvu jednadžbu: 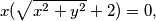 iz čega proizlazi da je
iz čega proizlazi da je 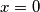 ili
ili 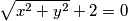 . Valja primijeti kako drugi slučaj nema smisla jer se dobije
. Valja primijeti kako drugi slučaj nema smisla jer se dobije 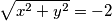 , a vrijednost korijena ne može biti negativan broj. Zapišimo matematičkim rječnikom:
, a vrijednost korijena ne može biti negativan broj. Zapišimo matematičkim rječnikom: 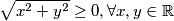 . Dakle, jedan i jedini uvjet je
. Dakle, jedan i jedini uvjet je 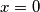 . Uvrstimo to u drugu jednadžbu:
. Uvrstimo to u drugu jednadžbu: 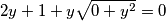
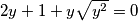
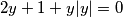 1. slučaj: ako je
1. slučaj: ako je 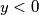 .
. 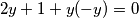
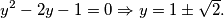 Pazimo da smo promatrali
Pazimo da smo promatrali 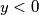 , tj. jedino rješenje ove jednadžbe je broj:
, tj. jedino rješenje ove jednadžbe je broj: 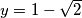 .
.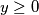 .
. 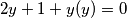
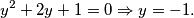 Pazimo da smo promatrali
Pazimo da smo promatrali 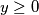 , tj. ovaj slučaj nema rješenja:
, tj. ovaj slučaj nema rješenja: 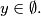
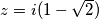 .
.  Školjka
Školjka