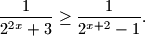Točno
8. kolovoza 2024. 17:09 (1 godina, 7 mjeseci)
Riješite jednadžbu
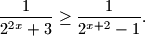
%V0
Riješite jednadžbu $$\frac{1}{2^{2x}+3} \ge \frac{1}{2^{x+2}-1}.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Sredimo nejednadžbu:
$$\frac{1}{({2^{x})}^{2} + 3} \geq \frac{1}{4\cdot2^{x}-1} .$$
Primijeti da možemo uvjeti supstituciju: $t = 2^{x}$ i nejednadžba poprima oblik:
$$\frac{1}{ t^{2} + 3} \geq \frac{1}{4t-1}$$
$$\frac{1}{ t^{2} + 3} - \frac{1}{4t-1} \geq 0$$
$$\frac{4t-1 - (t^{2} + 3)}{(t^{2} + 3)(4t-1)}\geq 0$$
$$\frac{4t-1 - t^{2} - 3}{(t^{2} + 3)(4t-1)}\geq 0$$
$$\frac{- t^{2} + 4t - 4}{(t^{2} + 3)(4t-1)}\geq 0$$
$$\frac{- (t^{2} - 4t + 4)}{(t^{2} + 3)(4t-1)}\geq 0$$
$$\frac{- (t - 2)^{2}}{(t^{2} + 3)(4t-1)}\geq 0$$
$$\frac{(t - 2)^{2}}{(t^{2} + 3)(4t-1)}\leq 0$$
Valja primijeti kako $t^{2} + 3 > 0 \Rightarrow t^{2} > -3 $ vrijedi za bilo koju vrijednost $t$ odnosno $2^{x}$. Dakle, $2^{x} + 3 \geq 0, \forall x \in \mathbb{R}$. Međutim, sličnu situaciju imamo i u brojniku: $(t-2)^{2} \geq 0, \forall t \in \mathbb{R}$, tj. $(2^{x}-2)^{2} \geq 0, \forall x \in \mathbb{R}$. Ali pazi! Pošto se postiže jednakost za $t = 0$, tj. za $2^{x} = 2 \Rightarrow x = 1$ to rješenje moramo uključiti u krajnje rješenje. Međutim, ako bi bila stroga nejednakost (strogo veće ili strogo manje), tada bi to rješenje morali isključiti. Nejednadžba poprima oblik:
$$\frac{1}{4t-1}\leq 0.$$
Brojnik je uvijek pozitivan što znači da bi vrijednost cijelog razlomka bila negativna ili jednaka nuli, nazivnik mora biti strogo manji od nule (jer "+" dijeljeno "-" daje "-"). Strogo je manji jer se nalazi u nazivniku, a on ne može biti jednak nuli. Prema tome:
$$4t-1 < 0 \Rightarrow t < \frac{1}{4} \Rightarrow 2^{x} < 2^{-2} \Rightarrow {x} < -2.$$
Nemojmo zaboraviti i rješenje $x = 1$. Rješenje nejednadžbe je: $x\in \langle -\infty, -2 \rangle \cup \{ 1\}$.
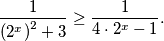 Primijeti da možemo uvjeti supstituciju:
Primijeti da možemo uvjeti supstituciju: 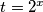 i nejednadžba poprima oblik:
i nejednadžba poprima oblik: 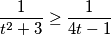
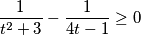
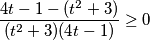
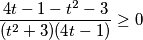
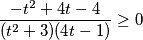
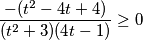
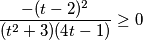
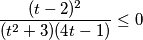 Valja primijeti kako
Valja primijeti kako 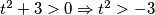 vrijedi za bilo koju vrijednost
vrijedi za bilo koju vrijednost  odnosno
odnosno 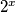 . Dakle,
. Dakle, 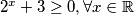 . Međutim, sličnu situaciju imamo i u brojniku:
. Međutim, sličnu situaciju imamo i u brojniku: 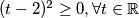 , tj.
, tj. 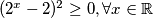 . Ali pazi! Pošto se postiže jednakost za
. Ali pazi! Pošto se postiže jednakost za 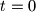 , tj. za
, tj. za 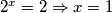 to rješenje moramo uključiti u krajnje rješenje. Međutim, ako bi bila stroga nejednakost (strogo veće ili strogo manje), tada bi to rješenje morali isključiti. Nejednadžba poprima oblik:
to rješenje moramo uključiti u krajnje rješenje. Međutim, ako bi bila stroga nejednakost (strogo veće ili strogo manje), tada bi to rješenje morali isključiti. Nejednadžba poprima oblik: 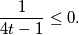 Brojnik je uvijek pozitivan što znači da bi vrijednost cijelog razlomka bila negativna ili jednaka nuli, nazivnik mora biti strogo manji od nule (jer "+" dijeljeno "-" daje "-"). Strogo je manji jer se nalazi u nazivniku, a on ne može biti jednak nuli. Prema tome:
Brojnik je uvijek pozitivan što znači da bi vrijednost cijelog razlomka bila negativna ili jednaka nuli, nazivnik mora biti strogo manji od nule (jer "+" dijeljeno "-" daje "-"). Strogo je manji jer se nalazi u nazivniku, a on ne može biti jednak nuli. Prema tome: 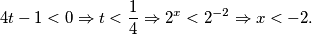 Nemojmo zaboraviti i rješenje
Nemojmo zaboraviti i rješenje 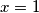 . Rješenje nejednadžbe je:
. Rješenje nejednadžbe je: 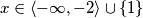 .
.  Školjka
Školjka