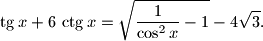Sredimo jednadžbu koristeći se trigonometrijskim identitetima. Savjet: nemojte odmah izražavati sve preko $\sin x$ i $\cos x$. Možda će to bespotrebno zakomplicirati zadatak.
$$\tg x + 6\ctg x= \sqrt{\frac{1-\cos^{2} x}{\cos^{2} x}} - 4 \sqrt{3}$$
$$\tg x + 6\frac{1}{\tg x}= \sqrt{\frac{\sin^{2} x}{\cos^{2} x}} - 4 \sqrt{3}$$
$$\tg x + 6\frac{1}{\tg x}= \sqrt{\tg^{2}x} - 4 \sqrt{3}$$
$$\tg x + \frac{6}{\tg x}= |\tg{x}|- 4 \sqrt{3}$$
Sada imamo jednadžbu s apsolutnom vrijednosti. \\
1. slučaj: $\tg x < 0 \Rightarrow x \in \langle \frac{\pi}{2} + k\pi, \pi + k\pi\rangle, k\in \mathbb{Z} $\\
Jednadžba poprima oblik:
$$\tg x + \frac{6}{\tg x}= -\tg{x}- 4 \sqrt{3}$$
$$2\tg x + \frac{6}{\tg x} + 4 \sqrt{3} = 0$$
$$2\tg^{2} x + 4 \sqrt{3} \tg x + 6 = 0$$
Uvedemo supstituciju $t = \tg x$ (radi jednostavnosti):
$$2t^{2} + 4 \sqrt{3}t + 6 = 0$$
$$t^{2} + 2\sqrt{3}t + 3= 0$$
$$(t+\sqrt{3})^{2}= 0 \Rightarrow t = -\sqrt{3} \Rightarrow \tg{x} = -\sqrt{3} \Rightarrow {x} = \frac{2\pi}{3} + k\pi, k\in \mathbb{Z}.$$
Pazi, promatrali smo samo $x \in \langle \frac{\pi}{2} + k\pi, \pi + k\pi\rangle, k\in \mathbb{Z}$ što nas dovodi do zaključka da je rješenje prvog slučaja ${x} = \frac{2\pi}{3} + k\pi, k\in \mathbb{Z}$.\\
2. slučaj: $\tg x > 0 \Rightarrow x \in \langle0 + k\pi,\frac{\pi}{2} + k\pi\rangle, k\in \mathbb{Z} $\\
Jednadžba poprima oblik:
$$\tg x + \frac{6}{\tg x}= \tg{x}- 4 \sqrt{3}$$
$$ \frac{6}{\tg x} = - 4 \sqrt{3}$$
$$\tg{x} = -\frac{\sqrt{3}}{2}.$$
Naime, promatrali smo samo ako je $\tg x > 0$ što znači ma koji god da bio $x$, njegov tangens ne može biti negativan kao što je u ovom slučaju. Dakle, $x\in \emptyset.$\\
Konačno rješenje jednadžbe je: ${x} = \frac{2\pi}{3} + k\pi, k\in \mathbb{Z}$.\\
NAPOMENA: \\
Funkcija $\tg x$ nije definirana za $x = \frac{\pi}{2} + k\pi$, a funkcija $\ctg x$ za $x =k\pi$, gdje je $k$ cijeli broj. Zato nije ni potrebno pisati uvjete pri množenju jednadžbe s $\tg x$ u oba slučaja jer je on jednak nuli baš onda kad $\ctg x$ nije definiran. Ali vrijedi i obrat: budući da $\ctg x$ nije definiran onda kad je $\tg x$ jednak nuli, tada pri "rastavljanju" na slučajeve kod jednadžbe s apsolutnom vrijednošću smo imali uvjete da je $\tg x$ strogo veći, odnosno strogo manji od nule. Dakle, uvjet prije rješavanja jednadžbe je $x \neq \frac{k\pi}{2}, k\in\mathbb{Z}.$
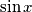 i
i 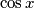 . Možda će to bespotrebno zakomplicirati zadatak.
. Možda će to bespotrebno zakomplicirati zadatak. 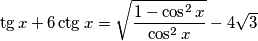
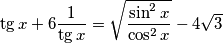
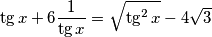
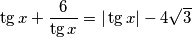 Sada imamo jednadžbu s apsolutnom vrijednosti.
Sada imamo jednadžbu s apsolutnom vrijednosti. 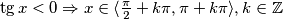
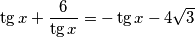
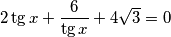
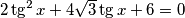 Uvedemo supstituciju
Uvedemo supstituciju 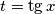 (radi jednostavnosti):
(radi jednostavnosti): 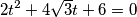
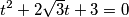
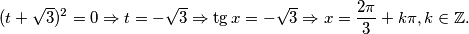 Pazi, promatrali smo samo
Pazi, promatrali smo samo 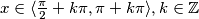 što nas dovodi do zaključka da je rješenje prvog slučaja
što nas dovodi do zaključka da je rješenje prvog slučaja 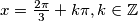 .
.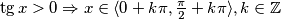
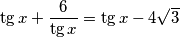
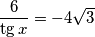
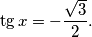 Naime, promatrali smo samo ako je
Naime, promatrali smo samo ako je 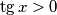 što znači ma koji god da bio
što znači ma koji god da bio  , njegov tangens ne može biti negativan kao što je u ovom slučaju. Dakle,
, njegov tangens ne može biti negativan kao što je u ovom slučaju. Dakle, 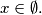
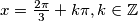 .
.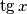 nije definirana za
nije definirana za 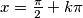 , a funkcija
, a funkcija 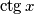 za
za 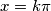 , gdje je
, gdje je  cijeli broj. Zato nije ni potrebno pisati uvjete pri množenju jednadžbe s
cijeli broj. Zato nije ni potrebno pisati uvjete pri množenju jednadžbe s 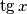 u oba slučaja jer je on jednak nuli baš onda kad
u oba slučaja jer je on jednak nuli baš onda kad 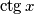 nije definiran. Ali vrijedi i obrat: budući da
nije definiran. Ali vrijedi i obrat: budući da 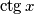 nije definiran onda kad je
nije definiran onda kad je 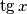 jednak nuli, tada pri "rastavljanju" na slučajeve kod jednadžbe s apsolutnom vrijednošću smo imali uvjete da je
jednak nuli, tada pri "rastavljanju" na slučajeve kod jednadžbe s apsolutnom vrijednošću smo imali uvjete da je 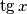 strogo veći, odnosno strogo manji od nule. Dakle, uvjet prije rješavanja jednadžbe je
strogo veći, odnosno strogo manji od nule. Dakle, uvjet prije rješavanja jednadžbe je 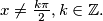
 Školjka
Školjka