Točno
12. prosinca 2023. 16:40 (2 godine, 2 mjeseci)
Odredi sve realne brojeve  za koje vrijede nejednakosti
za koje vrijede nejednakosti 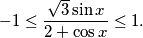
Odredi sve realne brojeve $x$ za koje vrijede nejednakosti
$$- 1 \leq \frac{\sqrt{3}\sin{x}}{2 + \cos{x}} \leq 1.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Rastavimo početnu nejednakost na dvije nejednadžbe koje nam čine sustav:\\
1. nejednadžba:
$$\frac{\sqrt{3}\sin x}{2+\cos x} \geq -1$$
Primijeti kako u nazivniku imamo izraz takav da za svaki broj $x \in \mathbb{R}$ vrijedi: $\cos x + 2 > 0 \Rightarrow \cos x > -2$. Ta tvrdnja potječe iz tvrdnje da je funkcija $f(x) = \cos x$ omeđena, tj. za nju vrijedi: $f: \mathbb{R} \rightarrow [-1,1]$. Cijelu nejednadžbu možemo pomnožiti s nazivnikom s obzirom na to da znamo da je on uvijek pozitivan. Nejednadžba poprima oblik:
$$\sqrt{3}\sin x\geq -(2+\cos x)$$
$$\sqrt{3}\sin x\geq -2-\cos x$$
$$\sqrt{3}\sin x + \cos x \geq -2$$
$$2 (\frac{\sqrt{3}}{2}\sin x + \frac{1}{2}\cos x) \geq -2$$
$$\frac{\sqrt{3}}{2}\sin x + \frac{1}{2}\cos x \geq -1$$
$$ \sin (\frac{\pi}{3}) \sin x + \cos (\frac{\pi}{3})\cos x \geq -1$$
$$ \cos(x-\frac{\pi}{3}) \geq -1 \Rightarrow x\in\mathbb{R}$$
2. nejednadžba:
$$\frac{\sqrt{3}\sin x}{2+\cos x} \leq 1$$
$$\sqrt{3}\sin x \leq 2+\cos x$$
$$\sqrt{3}\sin x \leq 2+\cos x$$
$$\sqrt{3}\sin x - \cos x \leq 2$$
$$2(\frac{\sqrt{3}}{2}\sin x - \frac{1}{2}\cos x) \leq 2$$
$$\frac{\sqrt{3}}{2}\sin x - \frac{1}{2}\cos x \leq 1$$
$$ \sin (\frac{\pi}{3}) \sin x- \cos (\frac{\pi}{3})\cos x \leq 1$$
$$ -\cos(x+\frac{\pi}{3}) \leq 1$$
$$ \cos(x+\frac{\pi}{3}) \geq -1 \Rightarrow x\in\mathbb{R}$$
Tražimo presjek rješenja nejednadžbi. Dakle, rješenje su svi realni brojevi odnosno: $x\in\mathbb{R}$.\\
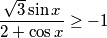 Primijeti kako u nazivniku imamo izraz takav da za svaki broj
Primijeti kako u nazivniku imamo izraz takav da za svaki broj 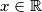 vrijedi:
vrijedi: 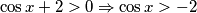 . Ta tvrdnja potječe iz tvrdnje da je funkcija
. Ta tvrdnja potječe iz tvrdnje da je funkcija 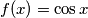 omeđena, tj. za nju vrijedi:
omeđena, tj. za nju vrijedi: ![f: \mathbb{R} \rightarrow [-1,1]](/media/m/6/5/6/6562f84516b21adc0e19d46601daea4b.png) . Cijelu nejednadžbu možemo pomnožiti s nazivnikom s obzirom na to da znamo da je on uvijek pozitivan. Nejednadžba poprima oblik:
. Cijelu nejednadžbu možemo pomnožiti s nazivnikom s obzirom na to da znamo da je on uvijek pozitivan. Nejednadžba poprima oblik: 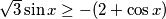
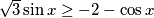
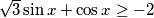
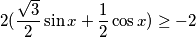
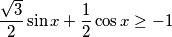
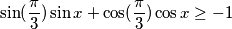
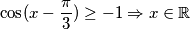 2. nejednadžba:
2. nejednadžba: 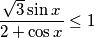
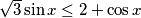
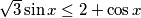
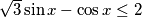
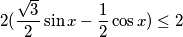
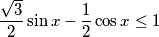
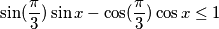
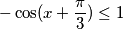
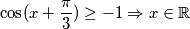 Tražimo presjek rješenja nejednadžbi. Dakle, rješenje su svi realni brojevi odnosno:
Tražimo presjek rješenja nejednadžbi. Dakle, rješenje su svi realni brojevi odnosno: 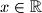 .
. Školjka
Školjka  za koje vrijede nejednakosti
za koje vrijede nejednakosti