Neocijenjeno
16. prosinca 2023. 14:23 (2 godine, 2 mjeseci)
Riješite nejednadžbu
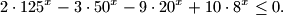
%V0
Riješite nejednadžbu $$
2\cdot 125^x-3\cdot 50^x-9\cdot 20^x+10\cdot 8^x\le 0.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Pojednostavnimo baze potencija. Nejednadžba poprima oblik:
$$2 \cdot 5^{3x} - 3 \cdot (5^{2} \cdot 2)^{x} - 9 \cdot (5 \cdot 2^{2})^{x} + 10 \cdot 2^{3x} \leq 0$$
$$2 \cdot 5^{3x} - 3 \cdot 5^{2x} \cdot 2^{x} - 9 \cdot 5^{x} \cdot 2^{2x} + 10 \cdot 2^{3x} \leq 0$$
Podijelimo cijelu nejednadžbu sa $5^{3x}$. Naime, pri dijeljenju sa $5^{3x}$ se ne moramo brinuti o predznaku (i okretanju znaka nejednakosti) s obzirom na to da je $5^{3x} > 0, \forall x \in \mathbb{R}$.
$$2 - 3 \cdot \frac{5^{2x} \cdot 2^{x}}{5^{3x}} - 9 \cdot \frac{5^{x} \cdot 2^{2x}}{5^{3x}} + 10 \cdot \frac{2^{3x}}{5^{3x}} \leq 0$$
$$2 - 3 \cdot \frac{2^{x}}{5^{x}} - 9 \cdot \frac{2^{2x}}{5^{2x}} + 10 \cdot \frac{2^{3x}}{5^{3x}} \leq 0$$
$$2 - 3 \cdot {\left( \frac{2}{5}\right)}^{x} - 9 \cdot \left({\left( \frac{2}{5}\right)}^{x}\right)^{2} + 10 \cdot \left({\left( \frac{2}{5}\right)}^{x}\right)^{3} \leq 0$$
Uvedimo supstituciju $t = {\left( \frac{2}{5}\right)}^{x}$. Nejednadžba poprima oblik:
$$2 - 3t- 9t^{2} + 10t^{3} \leq 0$$
$$10t^{3}- 9t^{2} - 3t + 2 \leq 0$$
$$10t^{3}- 10t^{2} + t^{2} - 3t + 2 \leq 0$$
$$10t^{2}(t-1)+ t^{2} - t - 2t + 2 \leq 0$$
$$10t^{2}(t-1)+ t (t-1) - 2(t -1) \leq 0$$
$$(t -1)(10t^{2}+ t - 2)\leq 0$$
$$(t -1)(10t^{2}+5t -4t - 2)\leq 0$$
$$(t -1)(5t(2t+1) -2(2t+1))\leq 0$$
$$(t -1)(5t-2)(2t+1)\leq 0$$
Rješenje ove nejednadžbe je:$ t \in \langle -\infty, -\frac{1}{2}] \cup \left[ \frac{2}{5}, 1 \right]$. Međutim, vratimo supstituciju $t = {\left( \frac{2}{5}\right)}^{x}$. Rješenje nejednadžbe se sada može zapisati u obliku: $ {\left( \frac{2}{5}\right)}^{x} \in \langle -\infty, -\frac{1}{2}]$ ili $ {\left( \frac{2}{5}\right)}^{x} \in \left[ \frac{2}{5}, 1 \right]$. Međutim, ta eksponencijalna funkcija poprima samo pozitivna vrijednosti, što znači da prvi slučaj nema rješenja jer ${\left( \frac{2}{5}\right)}^{x} \leq 0$ ne vrijedi ni za jedan realni broj. Slijedi da nam preostaje samo riješiti nejednadžbu: $\frac{2}{5} \leq {\left( \frac{2}{5}\right)}^{x} \leq 1$. Cijelu jednadžbu možemo logaritmirati po bazi $\frac{2}{5}$ pritom bazeći da se baza nalazi u intervalu $\langle 0, 1 \rangle$ te da se znak nejednakosti okreće:
$$\frac{2}{5} \leq {\left( \frac{2}{5}\right)}^{x} \leq 1 / \log_{\frac{2}{5}}$$
$$\log_{\frac{2}{5}}\left(\frac{2}{5}\right) \geq \log_{\frac{2}{5}}{{\left( \frac{2}{5}\right)}^{x}} \geq \log_{\frac{2}{5}}1$$
$$1 \geq x \geq 0.$$
Dakle, rješenje nejednadžbe je interval $[0,1]$.
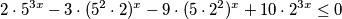
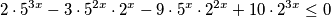 Podijelimo cijelu nejednadžbu sa
Podijelimo cijelu nejednadžbu sa 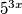 . Naime, pri dijeljenju sa
. Naime, pri dijeljenju sa 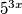 se ne moramo brinuti o predznaku (i okretanju znaka nejednakosti) s obzirom na to da je
se ne moramo brinuti o predznaku (i okretanju znaka nejednakosti) s obzirom na to da je 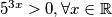 .
. 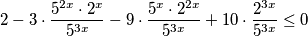
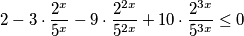
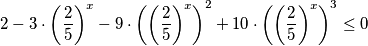 Uvedimo supstituciju
Uvedimo supstituciju 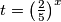 . Nejednadžba poprima oblik:
. Nejednadžba poprima oblik: 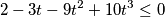
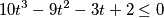
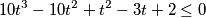
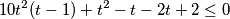

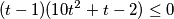
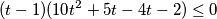
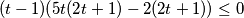
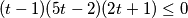 Rješenje ove nejednadžbe je:
Rješenje ove nejednadžbe je:![t \in \langle -\infty, -\frac{1}{2}] \cup \left[ \frac{2}{5}, 1 \right]](/media/m/d/3/f/d3fc346489d255968c884240a2bad72d.png) . Međutim, vratimo supstituciju
. Međutim, vratimo supstituciju 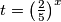 . Rješenje nejednadžbe se sada može zapisati u obliku:
. Rješenje nejednadžbe se sada može zapisati u obliku: ![{\left( \frac{2}{5}\right)}^{x} \in \langle -\infty, -\frac{1}{2}]](/media/m/e/1/f/e1f8e8c020f0283b8c1de6929a96bf81.png) ili
ili ![{\left( \frac{2}{5}\right)}^{x} \in \left[ \frac{2}{5}, 1 \right]](/media/m/0/d/3/0d324216568ce939c19e70539a9570f2.png) . Međutim, ta eksponencijalna funkcija poprima samo pozitivna vrijednosti, što znači da prvi slučaj nema rješenja jer
. Međutim, ta eksponencijalna funkcija poprima samo pozitivna vrijednosti, što znači da prvi slučaj nema rješenja jer 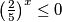 ne vrijedi ni za jedan realni broj. Slijedi da nam preostaje samo riješiti nejednadžbu:
ne vrijedi ni za jedan realni broj. Slijedi da nam preostaje samo riješiti nejednadžbu: 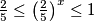 . Cijelu jednadžbu možemo logaritmirati po bazi
. Cijelu jednadžbu možemo logaritmirati po bazi  pritom bazeći da se baza nalazi u intervalu
pritom bazeći da se baza nalazi u intervalu 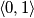 te da se znak nejednakosti okreće:
te da se znak nejednakosti okreće: 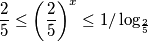
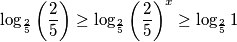
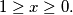 Dakle, rješenje nejednadžbe je interval
Dakle, rješenje nejednadžbe je interval ![[0,1]](/media/m/b/d/9/bd9184b120f6623b5154b311b9ae2f20.png) .
.  Školjka
Školjka