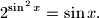Ovakav tip jednadžbi, kada imamo "miks" vrsta jednadžbi, rješava se traženjem minimuma ili maksimuma obje strane jednadžbe. U našem slučaju, neka je 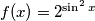 , a
, a 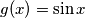 . Jednadžba se može zapisati u obliku
. Jednadžba se može zapisati u obliku 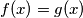 .
.
Promotrimo prvo jednostavniju funkciju 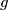 . Skup svih vrijednosti te funkcije je
. Skup svih vrijednosti te funkcije je ![[-1, 1]](/media/m/0/8/1/0818c98aa4a2936ddfb4e9eac7a862fe.png) , odnosno
, odnosno ![I_{g} = [-1, 1]](/media/m/a/1/8/a1834ee3967fc5bad3c3f1522e155490.png) .
.
Neka je 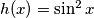 . Budući da je
. Budući da je 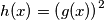 , funkcija će svaku vrijednost funkcije
, funkcija će svaku vrijednost funkcije 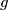 kvadrirati, odnosno može kvadrirati samo brojeve iz intervala
kvadrirati, odnosno može kvadrirati samo brojeve iz intervala ![[-1,1]](/media/m/8/d/9/8d92f93662539c83dd14147b1aec5197.png) . Dakle, ako je
. Dakle, ako je
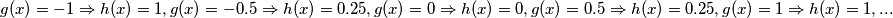 Vidimo da sve vrijednosti koje možemo dobiti od funkcije
Vidimo da sve vrijednosti koje možemo dobiti od funkcije  , odnosno skup svih vrijednosti funkcije
, odnosno skup svih vrijednosti funkcije  je zapravo interval
je zapravo interval ![[0,1]](/media/m/b/d/9/bd9184b120f6623b5154b311b9ae2f20.png) , tj.
, tj. ![I_{h} = [0, 1]](/media/m/5/7/9/5795001413823ba7ec1dd639ec355390.png) . Nadalje, ako je minimalna vrijednost funkcije
. Nadalje, ako je minimalna vrijednost funkcije  jednaka
jednaka  , onda je najmanja vrijednost funkcije
, onda je najmanja vrijednost funkcije  upravo
upravo 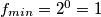 , a najveća onda kada je vrijednost funkcije
, a najveća onda kada je vrijednost funkcije  jednaka
jednaka  , tj.
, tj. 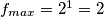 . Prema tome, slika funkcije
. Prema tome, slika funkcije  je
je ![I_{f} = [1,2]](/media/m/2/f/2/2f297a47cd9b5c2053adea442ada8b34.png) .
.
Sad se vratimo na početnu jednadžbu 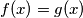 , a ta se jednakost može jedino postići ako i samo ako je
, a ta se jednakost može jedino postići ako i samo ako je 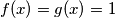 jer je to jedina vrijednost funkcija koju poprimaju, a da je zajednička. Sada moramo provjeriti poprimaju li tu vrijednost za isti
jer je to jedina vrijednost funkcija koju poprimaju, a da je zajednička. Sada moramo provjeriti poprimaju li tu vrijednost za isti  . Ako nisu, jednadžba nema rješenja i obrnuto.
. Ako nisu, jednadžba nema rješenja i obrnuto. 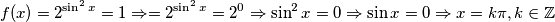
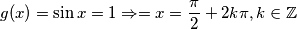 Dakle, ne postižu istu vrijednost za isti argument. Jednadžba nema rješenja, odnosno:
Dakle, ne postižu istu vrijednost za isti argument. Jednadžba nema rješenja, odnosno: 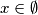 .
.
Ovakav tip jednadžbi, kada imamo "miks" vrsta jednadžbi, rješava se traženjem minimuma ili maksimuma obje strane jednadžbe. U našem slučaju, neka je $f(x) = 2^{\sin^{2}x}$, a $g(x) = \sin x$. Jednadžba se može zapisati u obliku $f(x) = g(x)$.\\
Promotrimo prvo jednostavniju funkciju $g$. Skup svih vrijednosti te funkcije je $[-1, 1]$, odnosno $I_{g} = [-1, 1]$.\\
Neka je $h(x) = \sin^{2}x$. Budući da je $h(x)=\left(g(x)\right)^{2}$, funkcija će svaku vrijednost funkcije $g$ kvadrirati, odnosno može kvadrirati samo brojeve iz intervala $[-1,1]$. Dakle, ako je \\
$$g(x) = -1 \Rightarrow h(x) = 1, g(x) = -0.5 \Rightarrow h(x) = 0.25, g(x) = 0 \Rightarrow h(x) = 0, g(x) = 0.5 \Rightarrow h(x) = 0.25, g(x) = 1 \Rightarrow h(x) = 1, ...$$
Vidimo da sve vrijednosti koje možemo dobiti od funkcije $h$, odnosno skup svih vrijednosti funkcije $h$ je zapravo interval $[0,1]$, tj. $I_{h} = [0, 1]$.
Nadalje, ako je minimalna vrijednost funkcije $h$ jednaka $0$, onda je najmanja vrijednost funkcije $f$ upravo $f_{min}=2^{0} = 1$, a najveća onda kada je vrijednost funkcije $h$ jednaka $1$, tj. $f_{max}=2^{1} = 2$. Prema tome, slika funkcije $f$ je $I_{f} = [1,2]$.\\
Sad se vratimo na početnu jednadžbu $f(x) = g(x)$, a ta se jednakost može jedino postići ako i samo ako je $f(x) = g(x) = 1$ jer je to jedina vrijednost funkcija koju poprimaju, a da je zajednička. Sada moramo provjeriti poprimaju li tu vrijednost za isti $x$. Ako nisu, jednadžba nema rješenja i obrnuto.
$$f(x) = 2^{\sin^{2}x} = 1 \Rightarrow = 2^{\sin^{2}x} = 2^0 \Rightarrow \sin^{2}x = 0 \Rightarrow \sin x = 0 \Rightarrow x = k\pi, k\in\mathbb{Z}$$
$$g(x) = \sin x = 1 \Rightarrow = x = \frac{\pi}{2} + 2k\pi, k\in\mathbb{Z}$$
Dakle, ne postižu istu vrijednost za isti argument. Jednadžba nema rješenja, odnosno: $x\in\emptyset$.
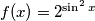 , a
, a 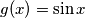 . Jednadžba se može zapisati u obliku
. Jednadžba se može zapisati u obliku 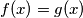 .
.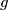 . Skup svih vrijednosti te funkcije je
. Skup svih vrijednosti te funkcije je ![[-1, 1]](/media/m/0/8/1/0818c98aa4a2936ddfb4e9eac7a862fe.png) , odnosno
, odnosno ![I_{g} = [-1, 1]](/media/m/a/1/8/a1834ee3967fc5bad3c3f1522e155490.png) .
.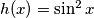 . Budući da je
. Budući da je 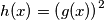 , funkcija će svaku vrijednost funkcije
, funkcija će svaku vrijednost funkcije 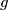 kvadrirati, odnosno može kvadrirati samo brojeve iz intervala
kvadrirati, odnosno može kvadrirati samo brojeve iz intervala ![[-1,1]](/media/m/8/d/9/8d92f93662539c83dd14147b1aec5197.png) . Dakle, ako je
. Dakle, ako je 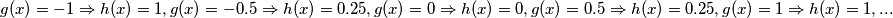 Vidimo da sve vrijednosti koje možemo dobiti od funkcije
Vidimo da sve vrijednosti koje možemo dobiti od funkcije  , odnosno skup svih vrijednosti funkcije
, odnosno skup svih vrijednosti funkcije  je zapravo interval
je zapravo interval ![[0,1]](/media/m/b/d/9/bd9184b120f6623b5154b311b9ae2f20.png) , tj.
, tj. ![I_{h} = [0, 1]](/media/m/5/7/9/5795001413823ba7ec1dd639ec355390.png) . Nadalje, ako je minimalna vrijednost funkcije
. Nadalje, ako je minimalna vrijednost funkcije  jednaka
jednaka  , onda je najmanja vrijednost funkcije
, onda je najmanja vrijednost funkcije  upravo
upravo 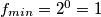 , a najveća onda kada je vrijednost funkcije
, a najveća onda kada je vrijednost funkcije  jednaka
jednaka  , tj.
, tj. 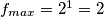 . Prema tome, slika funkcije
. Prema tome, slika funkcije  je
je ![I_{f} = [1,2]](/media/m/2/f/2/2f297a47cd9b5c2053adea442ada8b34.png) .
.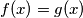 , a ta se jednakost može jedino postići ako i samo ako je
, a ta se jednakost može jedino postići ako i samo ako je 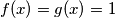 jer je to jedina vrijednost funkcija koju poprimaju, a da je zajednička. Sada moramo provjeriti poprimaju li tu vrijednost za isti
jer je to jedina vrijednost funkcija koju poprimaju, a da je zajednička. Sada moramo provjeriti poprimaju li tu vrijednost za isti  . Ako nisu, jednadžba nema rješenja i obrnuto.
. Ako nisu, jednadžba nema rješenja i obrnuto. 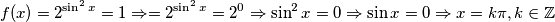
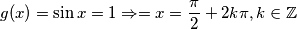 Dakle, ne postižu istu vrijednost za isti argument. Jednadžba nema rješenja, odnosno:
Dakle, ne postižu istu vrijednost za isti argument. Jednadžba nema rješenja, odnosno: 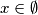 .
.  Školjka
Školjka