Neocijenjeno
22. veljače 2024. 20:19 (2 godine)
Dokaži da je, za sve

, broj
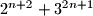
djeljiv sa

.
%V0
Dokaži da je, za sve $n \in \mathbb{N}$, broj $2^{n+2}+3^{2n+1}$ djeljiv sa $7$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Jedan klasični zadatak koji se rješava matematičkom indukcijom.\\
Neka je $f(n)=2^{n+2} + 3^{2n+1}, n\in\mathbb{N}$. Krenimo na matematičku indukciju:\\
1. BAZA indukcije
$$f(1) = 2^{1+2} + 3^{2\cdot 1 +1} = 8 + 27 = 35$$
Budući da $7$ dijeli $35$, baza indukcije vrijedi.\\
2. PRETPOSTAVKA indukcije: Pretpostavimo da je dani izraz djeljiv sa $7$ za $\forall n\in\mathbb{N}$.\\
S obzirom na to da je izraz djeljiv sa $7$, onda možemo napisati $f(n)=2^{n+2} + 3^{2n+1}=7k, k\in\mathbb{N}$.\\
3. KORAK indukcije:
$$f(n+1) = 2^{(n+1)+2} + 3^{2(n+1)+1}$$
$$f(n+1) = 2^{n+3} + 3^{2n+3}$$
$$f(n+1) = 2^{n+2} \cdot 2^{1} + 3^{2n+1} \cdot 3^{2}$$
$$f(n+1) = 2\cdot 2^{n+2} + 9 \cdot 3^{2n+1}$$
$$f(n+1) = 2\cdot 2^{n+2} + 2 \cdot 3^{2n+1} + 7 \cdot 3^{2n+1}$$
$$f(n+1) = 2\left(2^{n+2} + 3^{2n+1}\right) + 7 \cdot 3^{2n+1}$$
Uvrstimo li pretpostavku indukcije, dobijemo:
$$f(n+1) = 2\cdot 7k + 7 \cdot 3^{2n+1}$$
$$f(n+1) = 7\left(2k + 3^{2n+1}\right),$$
čime je dokaz završen.
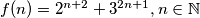 . Krenimo na matematičku indukciju:
. Krenimo na matematičku indukciju: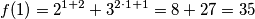 Budući da
Budući da  dijeli
dijeli 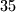 , baza indukcije vrijedi.
, baza indukcije vrijedi. za
za 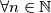 .
. , onda možemo napisati
, onda možemo napisati 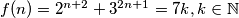 .
.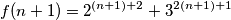
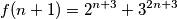
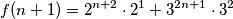
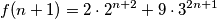
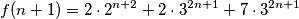
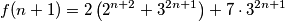 Uvrstimo li pretpostavku indukcije, dobijemo:
Uvrstimo li pretpostavku indukcije, dobijemo: 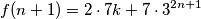
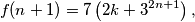 čime je dokaz završen.
čime je dokaz završen.  Školjka
Školjka  , broj
, broj 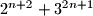 djeljiv sa
djeljiv sa