Točno
7. listopada 2013. 04:36 (12 godine, 5 mjeseci)
Ako je
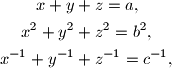
odredite
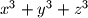
.
%V0
Ako je $$$\begin{align*}
x+y&+z=a,\\
x^2+y^2&+z^2=b^2,\\
x^{-1}+y^{-1}&+z^{-1}=c^{-1},
\end{align*}$$$ odredite $x^3+y^3+z^3$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$a^2 = x^2 + y^2 + z^2 + 2xy + 2xz + 2yz = b^2 + 2xy + 2xz + 2yz$
$xy+yz+zx = \frac{a^2-b^2}{2}$
$\frac{a^2-b^2}{2} = xyz \cdot (x^{-1} + y^{-1} + z^{-1}) = xyz \cdot c^{-1}$
$xyz = \frac{a^2c - b^2c}{2}$
$x^3+y^3+z^3 =$
$= (x^3 + y^3 + z^3 - 3xyz) + 3xyz = $
$= (x+y+z)(x^2+y^2+z^2 - xy-xz-yz) + 3xyz=$
$=a(b^2-\frac{a^2-b^2}{2})+3 \frac{a^2c - b^2c}{2}$
| 16. studenoga 2013. 21:57 | grga | Točno |