Točno
9. listopada 2013. 22:33 (12 godine, 5 mjeseci)
Neka je

realan broj takav da je
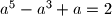
. Dokažite da vrijede nejednakosti
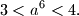
%V0
Neka je $a$ realan broj takav da je $a^5-a^3+a=2$. Dokažite da vrijede nejednakosti $$
3<a^6<4.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$a^5-a^3+a=2$
$a(a^4-a^2+1)=2$
$\frac{2}{a} = a^4-a^2+1 \geqslant a^2 \geqslant 0$ dakle $a \geqslant 0$
$2 = a^5-a^3+a \geqslant a^3$
$4 \geqslant a^6$
$a(a^4-a^2+1)=2$
$a \cdot \frac{a^6 + 1}{a^2 + 1} = 2$
$a^6 + 1 = 2 \cdot \frac{a^2 + 1}{a} \geqslant 2 \cdot \frac {2a}{a} = 4$
$a^6 \geqslant 3$
$3 \leqslant a^6 \leqslant 4$
Slucajeve jednakosti je lagano eliminirati zbog AG nejednakosti.
$3 < a^6 < 4$
| 16. studenoga 2013. 22:02 | grga | Točno |