Točno
10. listopada 2013. 00:07 (10 godine, 6 mjeseci)
Neka su
,
i
pozitivni realni brojevi za koje vrijedi
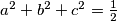
. Dokaži nejednakost
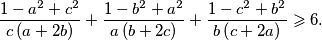
%V0
Neka su $a$, $b$ i $c$ pozitivni realni brojevi za koje vrijedi $a^2 + b^2 + c^2 = \frac{1}{2}$. Dokaži nejednakost $$ \frac{1 - a^2 + c^2}{c\left(a + 2 b\right)} + \frac{1 - b^2 + a^2}{a \left(b + 2 c\right)} + \frac{1 - c^2 + b^2}{b \left(c + 2 a\right)} \geqslant 6 \text{.} $$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$\sum\limits_{cyc}{ \frac{1 - a^2 + c^2}{c(a + 2b)} } \geqslant 6$
$\sum\limits_{cyc}{ \frac{a^2 + 2b^2 + 3c^2}{c(a + 2b)} } \geqslant 6$
$\sum\limits_{cyc}{ \frac{a^2 + 2b^2 + 3c^2}{c(a + 2b)} - 2} \geqslant 0$
$\sum\limits_{cyc}{ \frac{a^2 + 2b^2 + 3c^2 - 2ac - 4bc}{c(a + 2b)} } \geqslant 0$
$\sum\limits_{cyc}{ \frac{(a - c)^2 + 2(b - c)^2}{c(a + 2b)} } \geqslant 0$
Sto ocito vrijedi (brojnik je nenegativan, nazivnik je pozitivan zbog uvjeta zadatka)
| 16. studenoga 2013. 22:04 | grga | Točno |
| 5. studenoga 2016. 15:37 | nolo_moses | Točno |
Školjka 
