ikicic, 24. veljače 2015. 21:24
Dobro je rjesenje. Samo fale zagrade kod sume
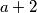
u predzadnjem redu, pa je mozda zato bilo zbunjujuce.
%V0
Dobro je rjesenje. Samo fale zagrade kod sume $a + 2$ u predzadnjem redu, pa je mozda zato bilo zbunjujuce.
ivl, 24. veljače 2015. 17:47
mozes malo objasnit zadnja 2 reda, ne shvacam bas sto je pretpostavljeno a sto dokazano.
Sori, dakle dokazao sam suma(1/a) >= 3 i suma(1/(a+2)) >= 1 time sto sam lupio CSB na (a,b,c) i (1/a,1/b,1/c) (analogno za a+2), pa ak zbrojimo te 2 stvarcice dobijemo originalnu nejednakost
%V0
[quote]mozes malo objasnit zadnja 2 reda, ne shvacam bas sto je pretpostavljeno a sto dokazano.[/quote]
Sori, dakle dokazao sam suma(1/a) >= 3 i suma(1/(a+2)) >= 1 time sto sam lupio CSB na (a,b,c) i (1/a,1/b,1/c) (analogno za a+2), pa ak zbrojimo te 2 stvarcice dobijemo originalnu nejednakost
grga, 16. studenoga 2013. 22:22
mozes malo objasnit zadnja 2 reda, ne shvacam bas sto je pretpostavljeno a sto dokazano.
%V0
mozes malo objasnit zadnja 2 reda, ne shvacam bas sto je pretpostavljeno a sto dokazano.