Neka je točka 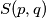 središte, a
središte, a  radijus tražene kružnice. Označimo pravce:
radijus tražene kružnice. Označimo pravce: 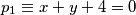 ,
, 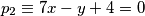 ,
, 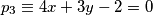 .
.
Iz uvjeta za tangentu kružnice, slijedi:
(1) iskoristimo činjenicu da su 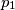 i
i 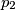 tangente na kružnicu.
tangente na kružnicu. 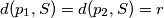
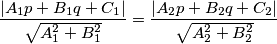
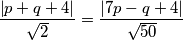
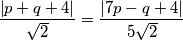
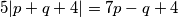 Dakle, imamo dvije mogućnosti:
Dakle, imamo dvije mogućnosti:
(1A) 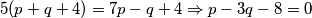 (1B)
(1B) 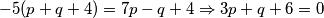 (2) iskoristimo to da vrijedi:
(2) iskoristimo to da vrijedi: 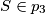 .
.
Za svaku točku na pravcu vrijedi 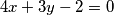 pa tako i za koordinate središte, tj.
pa tako i za koordinate središte, tj. 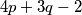 .
.
Dobijemo dva sustava jednadžbi što zavisi o tome koju jednadžbu iz 1 koristimo:
A: 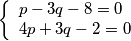 iz kojeg slijedi:
iz kojeg slijedi: 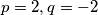 . Dakle,
. Dakle, 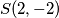 . Sada nam preostaje samo dobiti radijus
. Sada nam preostaje samo dobiti radijus  , a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi:
, a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi:
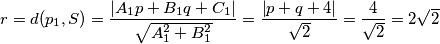 Rješenje A:
Rješenje A: 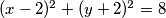 .
.
B: 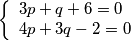 iz kojeg slijedi:
iz kojeg slijedi: 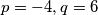 . Dakle,
. Dakle, 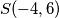 . Sada nam preostaje samo dobiti radijus
. Sada nam preostaje samo dobiti radijus  , a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi:
, a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi:
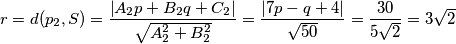 Rješenje B:
Rješenje B: 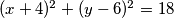 .
.
Dakle, tražene jednadžbe kružnica su: 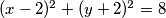 i
i 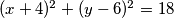 .
.
Neka je točka $S(p, q)$ središte, a $r$ radijus tražene kružnice. Označimo pravce: $p_{1} \equiv x+y +4 = 0$, $p_{2} \equiv 7x-y +4 = 0$, $p_{3} \equiv 4x+3y - 2 = 0$.\\
Iz uvjeta za tangentu kružnice, slijedi:\\
(1) iskoristimo činjenicu da su $p_{1}$ i $p_{2}$ tangente na kružnicu.
$$d(p_{1},S)=d(p_{2},S) = r$$
$$\frac{ \left |A_{1}p+B_{1}q+C_{1} \right |}{\sqrt{A_{1}^{2}+B_{1}^{2}}}=\frac{ \left |A_{2}p+B_{2}q+C_{2} \right |}{\sqrt{A_{2}^{2}+B_{2}^{2}}}$$
$$\frac{\left |p+q+4 \right |}{\sqrt{2}}=\frac{\left | 7p-q+4 \right|}{\sqrt{50}}$$
$$\frac{\left |p+q+4 \right |}{\sqrt{2}}=\frac{\left | 7p-q+4 \right|}{5\sqrt{2}}$$
$$5|p+q+4|=7p-q+4$$
Dakle, imamo dvije mogućnosti:\\
(1A) $$5(p+q+4)=7p-q+4 \Rightarrow p-3q-8=0$$
(1B) $$-5(p+q+4)=7p-q+4 \Rightarrow 3p+q+6=0$$
(2) iskoristimo to da vrijedi: $S \in p_{3}$. \\
Za svaku točku na pravcu vrijedi $4x+3y-2 = 0$ pa tako i za koordinate središte, tj. $4p+3q-2$.\\
Dobijemo dva sustava jednadžbi što zavisi o tome koju jednadžbu iz 1 koristimo: \\
A:
$$ \left\{\begin{array}{lr}
p - 3q - 8 = 0\\
4p + 3q - 2 = 0\\
\end{array}
\right. $$
iz kojeg slijedi: $p = 2, q = -2$. Dakle, $S(2, -2)$. Sada nam preostaje samo dobiti radijus $r$, a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi:\\
$$r = d(p_{1},S) = \frac{\left | A_{1}p+B_{1}q+C_{1} \right |}{\sqrt{A_{1}^{2}+B_{1}^{2}}} = \frac{\left | p+q+4 \right |}{\sqrt{2}} = \frac{4}{\sqrt{2}} = 2\sqrt{2}$$
Rješenje A: $(x-2)^{2}+(y+2)^{2} = 8$.\\
B:
$$ \left\{\begin{array}{lr}
3p + q + 6 = 0\\
4p + 3q - 2 = 0\\
\end{array}
\right. $$
iz kojeg slijedi: $p = -4, q = 6$. Dakle, $S(-4, 6)$. Sada nam preostaje samo dobiti radijus $r$, a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi:\\
$$r = d(p_{2},S) = \frac{ \left |A_{2}p+B_{2}q+C_{2} \right |}{\sqrt{A_{2}^{2}+B_{2}^{2}}} = \frac{\left |7p-q+4\right |}{\sqrt{50}} = \frac{30}{5\sqrt{2}} = 3\sqrt{2}$$
Rješenje B: $(x+4)^{2}+(y-6)^{2} = 18$.\\
Dakle, tražene jednadžbe kružnica su: $(x-2)^{2}+(y+2)^{2} = 8$ i $(x+4)^{2}+(y-6)^{2} = 18$.
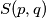 središte, a
središte, a  radijus tražene kružnice. Označimo pravce:
radijus tražene kružnice. Označimo pravce: 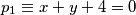 ,
, 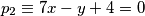 ,
, 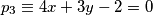 .
.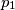 i
i 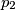 tangente na kružnicu.
tangente na kružnicu. 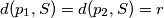
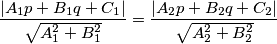
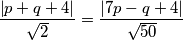
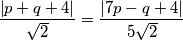
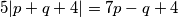 Dakle, imamo dvije mogućnosti:
Dakle, imamo dvije mogućnosti: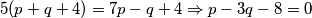 (1B)
(1B) 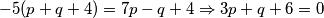 (2) iskoristimo to da vrijedi:
(2) iskoristimo to da vrijedi: 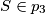 .
. 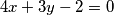 pa tako i za koordinate središte, tj.
pa tako i za koordinate središte, tj. 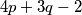 .
.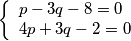 iz kojeg slijedi:
iz kojeg slijedi: 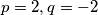 . Dakle,
. Dakle, 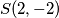 . Sada nam preostaje samo dobiti radijus
. Sada nam preostaje samo dobiti radijus  , a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi:
, a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi: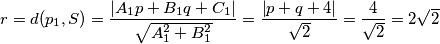 Rješenje A:
Rješenje A: 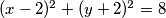 .
.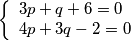 iz kojeg slijedi:
iz kojeg slijedi: 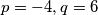 . Dakle,
. Dakle, 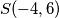 . Sada nam preostaje samo dobiti radijus
. Sada nam preostaje samo dobiti radijus  , a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi:
, a to možemo učiniti uvrštavanjem koordinata radijus u jednu od jednadžbi u (1). Slijedi: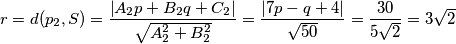 Rješenje B:
Rješenje B: 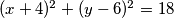 .
.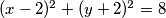 i
i 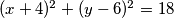 .
.  Školjka
Školjka 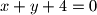 i
i 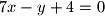 tangente su kružnice čije je središte na pravcu
tangente su kružnice čije je središte na pravcu 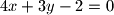 . Nađite jednadžbu te kružnice.
. Nađite jednadžbu te kružnice.