Neocijenjeno
22. veljače 2024. 20:50 (1 godina, 12 mjeseci)
Ako su

,

i

realni brojevi za koje je
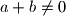
,
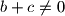
i
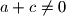
, dokaži da izraz:
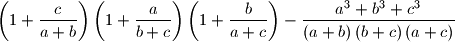
ne ovisi o vrijednostima brojeva

,

i

.
%V0
Ako su $a$, $b$ i $c$ realni brojevi za koje je $a+b\neq0$, $b+c\neq0$ i $a+c\neq0$, dokaži da izraz: $$
\left(1+\dfrac{c}{a+b}\right) \left( 1+\dfrac{a}{b+c}\right)
\left( 1+\dfrac{b}{a+c}\right) -\dfrac{a^{3}+b^{3}+c^{3}}
{\left(a+b\right) \left(b+c\right) \left(a+c\right)}
$$ ne ovisi o vrijednostima brojeva $a$, $b$ i $c$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Cilj nam je dokazati da je vrijednost ovog izraza konstanta. Drugim riječima, nakon što "sredimo" izraz, ne smije sadržavati brojeve $a$, $b$ i $c$.
$$ = \frac{a+b+c}{a+b} \cdot \frac{b+c+a}{b+c} \cdot \frac{a+c+b}{a+c} - \frac{a^{3}+b^{3}+c^{3}}{(a+b)(b+c)(a+c)} $$
$$ = \frac{a+b+c}{a+b} \cdot \frac{a+b+c}{b+c} \cdot \frac{a+b+c}{a+c} - \frac{a^{3}+b^{3}+c^{3}}{(a+b)(b+c)(a+c)} $$
$$ = \frac{(a+b+c)^{3}}{(a+b)(b+c)(a+c)} - \frac{a^{3}+b^{3}+c^{3}}{(a+b)(b+c)(a+c)} $$
$$ = \frac{(a+b+c)^{3}-(a^{3}+b^{3}+c^{3})}{(a+b)(b+c)(a+c)}$$
Izvest ćemo formulu na koji drugi način možemo izraziti $a^{3}+b^{3}+c^{3}$.
$$(a+b+c)^3 = ([a+b]+c)^3 = (a+b)^3 + 3(a+b)^2c +3(a+b)c^2 + c^3$$
$$(a+b+c)^3 = a^3 + 3a^2b+3ab^2+b^3 + c^3 + 3(a+b)c\cdot(a+b+c)$$
$$(a+b+c)^3 = a^3 +b^3 + c^3 + 3ab(a+b) + 3(a+b)c\cdot(a+b+c)$$
$$(a+b+c)^3 = a^3 +b^3 + c^3 + 3(a+b)\cdot(ab+c(a+b+c))$$
$$(a+b+c)^3 = a^3 +b^3 + c^3 + 3(a+b)\cdot(ab+ac+bc+c^2)$$
$$(a+b+c)^3 = a^3 +b^3 + c^3 + 3(a+b)\cdot(a(b+c)+c(b+c))$$
$$(a+b+c)^3 = a^3 +b^3 + c^3 + 3(a+b)(a+c)(b+c) \Rightarrow a^3 +b^3 + c^3 =(a+b+c)^3 - 3(a+b)(a+c)(b+c)$$
Uvrštavanjem u izraz, dobijemo:
$$ = \frac{(a+b+c)^{3}-((a+b+c)^3 - 3(a+b)(a+c)(b+c))}{(a+b)(b+c)(a+c)}$$
$$ = \frac{ 3(a+b)(a+c)(b+c)}{(a+b)(b+c)(a+c)} = 3$$
što je i trebalo dokazati. Vrijednost izraza je konstantna i iznosi $3$.