Označimo: 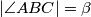 ,
, 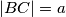 ,
, 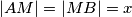 ,
, 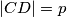 ,
, 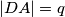 ,
, 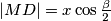 ,
, 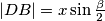
Iz poučka o simetrali kuta slijedi: 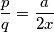 što treba pokazati da je jednako
što treba pokazati da je jednako  kako bismo dobili tvrdnju ekvivalentnu onoj u zadatku. Odavde ćemo izraziti
kako bismo dobili tvrdnju ekvivalentnu onoj u zadatku. Odavde ćemo izraziti 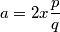 . Također, radi kraćeg pisanja, uvedimo supstituciju:
. Također, radi kraćeg pisanja, uvedimo supstituciju: 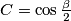
Iz poučka o kosinusu u trokutu 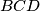 slijedi:
slijedi: 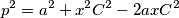 odnosno, kad uvrstimo
odnosno, kad uvrstimo  :
: 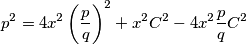 Iz poučka o kosinusu u trokutu
Iz poučka o kosinusu u trokutu  slijedi:
slijedi: 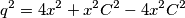
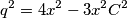 Dijeljenjem te dvije jednadžbe možemo izraziti
Dijeljenjem te dvije jednadžbe možemo izraziti 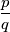 :
: 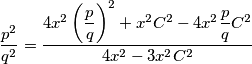 Sad uvrstimo supstituciju:
Sad uvrstimo supstituciju: 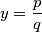 i riješimo kvadratnu jednadžbu za
i riješimo kvadratnu jednadžbu za  :
:
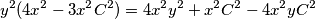
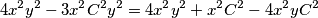
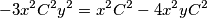
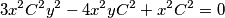
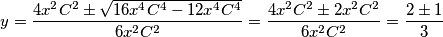 Primijetimo da ne može biti
Primijetimo da ne može biti 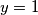 , jer to bi značilo da je
, jer to bi značilo da je 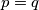 , odnosno trokut
, odnosno trokut  jednakokračan s osnovicom
jednakokračan s osnovicom  , pa je
, pa je 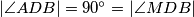 , odnosno
, odnosno 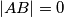 jer je
jer je 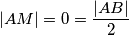 .
.
Zaključujemo da je 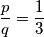 , što je trebalo dokazati.
, što je trebalo dokazati.
Označimo: $|\angle ABC| = \beta$, $|BC| = a$, $|AM| = |MB| = x$, $|CD| = p$, $|DA| = q$, $|MD| = x \cos \frac{\beta}2$, $|DB| = x \sin \frac{\beta}2$\\
Iz poučka o simetrali kuta slijedi: $$\dfrac{p}{q} = \dfrac{a}{2x}$$ što treba pokazati da je jednako $\frac13$ kako bismo dobili tvrdnju ekvivalentnu onoj u zadatku. Odavde ćemo izraziti $a = 2x\dfrac{p}{q}$. Također, radi kraćeg pisanja, uvedimo supstituciju: $C = \cos\frac{\beta}2$\\
Iz poučka o kosinusu u trokutu $BCD$ slijedi:
$$p^2 = a^2 + x^2C^2 - 2axC^2$$
odnosno, kad uvrstimo $a$:
$$p^2 = 4x^2\left(\frac{p}{q}\right)^2 + x^2C^2 - 4x^2\frac{p}{q}C^2$$
Iz poučka o kosinusu u trokutu $AMD$ slijedi:
$$q^2 = 4x^2 + x^2C^2 - 4x^2C^2$$
$$q^2 = 4x^2 - 3x^2C^2$$
Dijeljenjem te dvije jednadžbe možemo izraziti $\dfrac{p}{q}$:
$$\frac{p^2}{q^2} = \dfrac{4x^2\left(\dfrac{p}{q}\right)^2 + x^2C^2 - 4x^2\dfrac{p}{q}C^2}{4x^2 - 3x^2C^2}$$
Sad uvrstimo supstituciju: $y = \dfrac{p}{q}$ i riješimo kvadratnu jednadžbu za $y$:
$$y^2(4x^2-3x^2C^2) = 4x^2y^2 + x^2C^2 - 4x^2yC^2$$
$$4x^2y^2-3x^2C^2y^2 = 4x^2y^2 + x^2C^2 - 4x^2yC^2$$
$$-3x^2C^2y^2 = x^2C^2 - 4x^2yC^2$$
\\
$$3x^2C^2 y^2- 4x^2yC^2 + x^2C^2 = 0$$
$$y = \dfrac{4x^2C^2 \pm \sqrt{16x^4C^4 - 12x^4C^4}}{6x^2C^2} = \dfrac{4x^2C^2 \pm 2x^2C^2}{6x^2C^2} = \dfrac{2\pm1}{3}$$
Primijetimo da ne može biti $y = 1$, jer to bi značilo da je $p = q$, odnosno trokut $ABC$ jednakokračan s osnovicom $\overline{AC}$, pa je $|\angle ADB| = 90^{\circ} = |\angle MDB|$, odnosno $|AB| = 0$ jer je $|AM| = 0 = \dfrac{|AB|}2$.\\
Zaključujemo da je $\dfrac{p}{q} = \dfrac13$, što je trebalo dokazati.
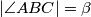 ,
, 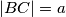 ,
, 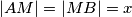 ,
, 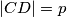 ,
, 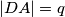 ,
, 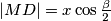 ,
, 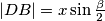
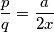 što treba pokazati da je jednako
što treba pokazati da je jednako  kako bismo dobili tvrdnju ekvivalentnu onoj u zadatku. Odavde ćemo izraziti
kako bismo dobili tvrdnju ekvivalentnu onoj u zadatku. Odavde ćemo izraziti 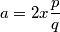 . Također, radi kraćeg pisanja, uvedimo supstituciju:
. Također, radi kraćeg pisanja, uvedimo supstituciju: 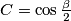
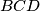 slijedi:
slijedi: 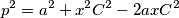 odnosno, kad uvrstimo
odnosno, kad uvrstimo  :
: 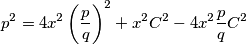 Iz poučka o kosinusu u trokutu
Iz poučka o kosinusu u trokutu  slijedi:
slijedi: 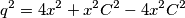
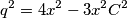 Dijeljenjem te dvije jednadžbe možemo izraziti
Dijeljenjem te dvije jednadžbe možemo izraziti 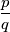 :
: 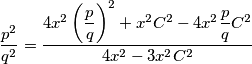 Sad uvrstimo supstituciju:
Sad uvrstimo supstituciju: 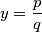 i riješimo kvadratnu jednadžbu za
i riješimo kvadratnu jednadžbu za  :
: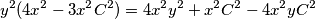
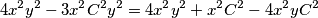
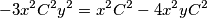
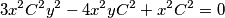
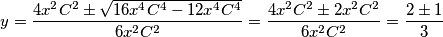 Primijetimo da ne može biti
Primijetimo da ne može biti 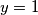 , jer to bi značilo da je
, jer to bi značilo da je 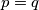 , odnosno trokut
, odnosno trokut  jednakokračan s osnovicom
jednakokračan s osnovicom  , pa je
, pa je 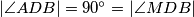 , odnosno
, odnosno 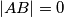 jer je
jer je 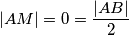 .
.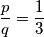 , što je trebalo dokazati.
, što je trebalo dokazati.  Školjka
Školjka  je polovište stranice
je polovište stranice  , a točka
, a točka  sjecište stranice
sjecište stranice 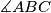 . Ako je
. Ako je 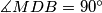 , dokaži da vrijedi
, dokaži da vrijedi 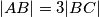 .
.