Točno
20. listopada 2013. 18:25 (12 godine, 4 mjeseci)
Sakrij rješenje
Dokaži pravilo o djeljivosti s

.
%V0
Dokaži pravilo o djeljivosti s $4$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Zapisimo broj kao
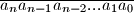
gdje su
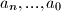
znamenke. Nazovimo ostatak koji taj broj daje pri djeljenju s


.
Tada je
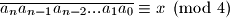
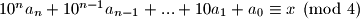
Kako je
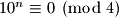
za
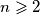
, nas izraz postaje
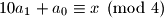
Dakle, ako promatramo zadnje dvije znamenke nekog broja kao zaseban broj, taj broj daje isti ostatak pri djeljenju s

kao pocetni broj.
%V0
Zapisimo broj kao $\overline{a_na_{n-1}a_{n-2}...a_1a_0}$ gdje su $ a_n,..., a_0$ znamenke. Nazovimo ostatak koji taj broj daje pri djeljenju s $4$ $x$.
Tada je $\overline{a_na_{n-1}a_{n-2}...a_1a_0} \equiv x \pmod 4$
$10^na_n + 10^{n-1}a_{n-1} + ... + 10a_1 + a_0 \equiv x \pmod 4$
Kako je $10^n \equiv 0 \pmod 4$ za $n \geqslant 2$, nas izraz postaje
$10a_1+a_0 \equiv x \pmod 4$
Dakle, ako promatramo zadnje dvije znamenke nekog broja kao zaseban broj, taj broj daje isti ostatak pri djeljenju s $4$ kao pocetni broj.
| 20. listopada 2013. 19:15 | ikicic | Točno |