Točno
20. listopada 2013. 19:30 (12 godine, 4 mjeseci)
Sakrij rješenje
Koliko je
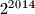
modulo

?
%V0
Koliko je $2^{2014}$ modulo $17$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
Broj $2^{2014}$ je znacajno prevelik da bi ga izracunao. Kako nemam bolje ideje, idem raspisati ostatke prvih nekoliko potencija broja $2$, mozda uocim nesto korisno.
$2^1 \equiv 2 \pmod {17}$
$2^2 \equiv 4 \pmod {17}$
$2^3 \equiv 8 \pmod {17}$
$2^4 \equiv 16 \pmod {17}$
$2^5 \equiv 15 \pmod {17}$
$2^6 \equiv 13 \pmod {17}$
$2^7 \equiv 9 \pmod {17}$
$2^8 \equiv 1 \pmod {17}$
Primjetimo da je $2^8 \equiv 1 \pmod {17}$
Kako je $2014=8*251+6$ broj $2^{2014}$ mozemo zapisati kao $(2^8)^{251}\cdot 2^6$
$2^{2014} \equiv x \pmod {17}$
$(2^8)^{251}\cdot 2^6 \equiv x \pmod {17}$
$1^{251} \cdot 2^6 \equiv x \pmod {17}$
$13 \equiv x \pmod {17}$
Ostatak $2^{2014}$ pri djeljenju s $17$ je $13$.
| 20. listopada 2013. 19:31 | ikicic | Točno |