Točno
20. listopada 2013. 19:02 (12 godine, 4 mjeseci)
Sakrij rješenje
Za koje cijele brojeve

je
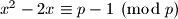
za neki prost broj

?
%V0
Za koje cijele brojeve $x$ je $x^2 -2x \equiv p-1 \pmod p$ za neki prost broj $p$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Znamo da mozemo na obje strane kongruencijske "jednadzbe" dodati isti broj, sto zapravo znaci da mozemo "prebacivati brojeve na drugu stranu".
Dakle, izraz postaje



Da bi kvadrat broja bio djeljiv s prostim

, i sam taj broj mora biti djeljiv s

. Dakle


%V0
Znamo da mozemo na obje strane kongruencijske "jednadzbe" dodati isti broj, sto zapravo znaci da mozemo "prebacivati brojeve na drugu stranu".
Dakle, izraz postaje
$x^2 - 2x +1 -p \equiv 0 \pmod p$
$x^2 -2x +1 \equiv 0 \pmod p$
$(x-1)^2 \equiv 0 \pmod p$
Da bi kvadrat broja bio djeljiv s prostim $p$, i sam taj broj mora biti djeljiv s $p$. Dakle
$x -1\equiv 0 \pmod p$
$x \equiv 1 \pmod p$
| 20. listopada 2013. 19:19 | ikicic | Točno |