Točno
20. listopada 2013. 19:36 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Prvo rjesenje: Prebacimo sve na istu stranu
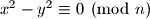
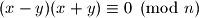
Iz ovoga se jasno vidi da je i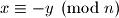 rjesenje.
rjesenje.
Naravno, potrebno je provjeriti je li moguce da je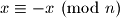 za sve
za sve  . Ako vrijedi za sve
. Ako vrijedi za sve  onda vrijedi i za
onda vrijedi i za 
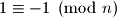
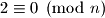
Dakle, ako je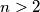 , nije nuzno, no za
, nije nuzno, no za  i
i je.
je.
Drugo rjesenje: Sjetimo se cinjenice da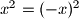 .
.
Ako su brojevi jednaki sigurno daju isti ostatak pri djeljenju sa bilo kojim brojem .
.
Ponovno, odmah je ocito da je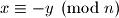 rjesenje.
rjesenje.
Naravno, potrebno je provjeriti je li moguce da je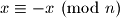 za sve
za sve  . Ako vrijedi za sve
. Ako vrijedi za sve  onda vrijedi i za
onda vrijedi i za 
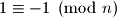
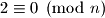
Dakle, ako je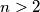 , nije nuzno, no za
, nije nuzno, no za  i
i je.
je.
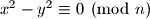
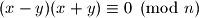
Iz ovoga se jasno vidi da je i
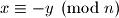 rjesenje.
rjesenje. Naravno, potrebno je provjeriti je li moguce da je
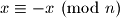 za sve
za sve  . Ako vrijedi za sve
. Ako vrijedi za sve  onda vrijedi i za
onda vrijedi i za 
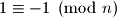
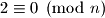
Dakle, ako je
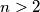 , nije nuzno, no za
, nije nuzno, no za  i
i je.
je.Drugo rjesenje: Sjetimo se cinjenice da
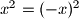 .
.Ako su brojevi jednaki sigurno daju isti ostatak pri djeljenju sa bilo kojim brojem
 .
.Ponovno, odmah je ocito da je
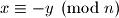 rjesenje.
rjesenje.Naravno, potrebno je provjeriti je li moguce da je
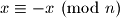 za sve
za sve  . Ako vrijedi za sve
. Ako vrijedi za sve  onda vrijedi i za
onda vrijedi i za 
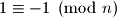
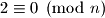
Dakle, ako je
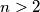 , nije nuzno, no za
, nije nuzno, no za  i
i je.
je.  Školjka
Školjka 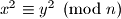 , je li nužno
, je li nužno 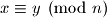 ?
?