Točno
20. listopada 2013. 19:37 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo da neka dva kvadrata daju isti ostatak modulo  .
.
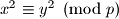
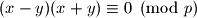
Da bi umozak dva broja bio djeljiv s prostim brojem , barem jedan od njih mora biti djeljiv s
, barem jedan od njih mora biti djeljiv s  .
.
Dakle ili vrijedi
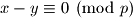
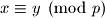
ili vrijedi
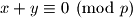
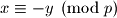
Dakle za svaki postoji tocno jedan broj
postoji tocno jedan broj  koji daje razlicit ostatak pri djeljenju s
koji daje razlicit ostatak pri djeljenju s  , ali ciji kvadrat daje isti ostatak. Naravno, moramo pipaziti na jednu iznimku, broj koji je djeljiv s
, ali ciji kvadrat daje isti ostatak. Naravno, moramo pipaziti na jednu iznimku, broj koji je djeljiv s  ima svojstvo da je
ima svojstvo da je 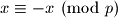 (to jest
(to jest 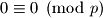 ). Dakle, brojevi djeljivi s
). Dakle, brojevi djeljivi s  nam daju jedan ostatak (
nam daju jedan ostatak ( ), a ostalih ima ukupno
), a ostalih ima ukupno 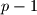 , i svaki ima svog para s kojim daje isti ostatak. Dakle ukupno imamo
, i svaki ima svog para s kojim daje isti ostatak. Dakle ukupno imamo 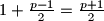 mogucih kvadratnih ostataka.
mogucih kvadratnih ostataka.
 .
.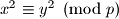
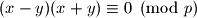
Da bi umozak dva broja bio djeljiv s prostim brojem
 , barem jedan od njih mora biti djeljiv s
, barem jedan od njih mora biti djeljiv s  .
. Dakle ili vrijedi
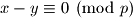
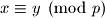
ili vrijedi
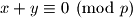
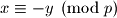
Dakle za svaki
 postoji tocno jedan broj
postoji tocno jedan broj  koji daje razlicit ostatak pri djeljenju s
koji daje razlicit ostatak pri djeljenju s  , ali ciji kvadrat daje isti ostatak. Naravno, moramo pipaziti na jednu iznimku, broj koji je djeljiv s
, ali ciji kvadrat daje isti ostatak. Naravno, moramo pipaziti na jednu iznimku, broj koji je djeljiv s  ima svojstvo da je
ima svojstvo da je 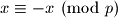 (to jest
(to jest 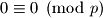 ). Dakle, brojevi djeljivi s
). Dakle, brojevi djeljivi s  nam daju jedan ostatak (
nam daju jedan ostatak ( ), a ostalih ima ukupno
), a ostalih ima ukupno 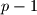 , i svaki ima svog para s kojim daje isti ostatak. Dakle ukupno imamo
, i svaki ima svog para s kojim daje isti ostatak. Dakle ukupno imamo 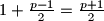 mogucih kvadratnih ostataka.
mogucih kvadratnih ostataka.  Školjka
Školjka 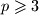 ?
?